|
||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
FONCTION
LOGIQUE "OU EXCLUSIF"
De deux choses: l’une ou l’autre mais pas les deux à la
fois Fromage ou dessert mais pas les
deux! |
Anglais: Exclusive
OR, abrégé en XOR
|
|
||||
|
Disjonction exclusive
|
||||
|
Simple
|
Évolué
|
Particulier
|
||
|
(Mathématiques
modernes) |
|
|||||
|
||||||
|
On
remarque que A
w B = (A sans B) OU (B sans A) Qui
se note A
w B = (A ET OU (B ET Rappel Le symbole |
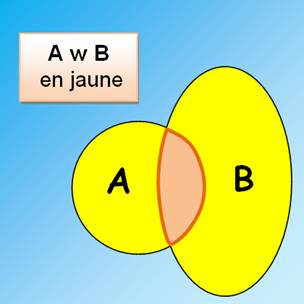
Diagramme de Venn
Voir Diagramme de Venn |
|||||
|
|
|||||||||||||||||
|
OU EXCLUSIF (XOR)
|
|||||||||||||||||
|
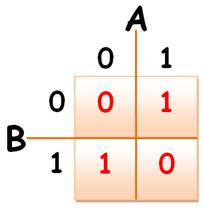
Table de vérité
Fonctions
|
Diagramme de
Karnaugh
|
||||||||||||||||
|
CIRCUITS LOGIQUES / ORDINATEURS |
|
|
|
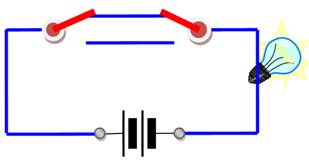
Circuit
électrique: va-et-vient
|
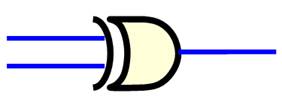
Circuit
électronique: porte ou-exclusif
|
|
|
|
||||||||||||||||||||||
|
Table
de vérité de l'addition
|
Addition
en binaire 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 On se souvient que 10 binaire vaut 2 en décimal. Circuit
logique
|
|||||||||||||||||||||
Voir Explications
détaillée et montage d'un additionneur complet
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Illustration
Exemple avec ensembles de
nombres
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fonction dans l'un mais dans aucun des autres
|
Le ou exclusifs sur trois variables élimine le "trèfle" sauf
sa partie centrale. Quelle est la fonction qui l'élimine aussi ?
|
|
|
||||||||||||||||||||||||||||||||
|
La sortie reste à zéro, bien
entendu!
|
Sur
un bit
Sur
un mot de n bits
|
|||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()