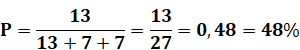|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Énigmes avec les FAMILLES Paradoxe des deux garçons ou
paradoxe des deux sœurs Probabilités garçons ou filles dans une famille de n enfants? En général ou lorsque certains enfants sont déjà là … Pas si évident qu'il y paraît à première vue. Ici, on suppose que la probabilité garçon ou
mille est égale (50/50) La probabilité de naître est la même quel que
soit le jour de naissance. Pas de naissances simultanées (jumeaux). |
Anglais: Siblings = fratrie /
Voir Paradoxes
|
|
||
|
M. Martin a deux enfants. L'ainé est un garçon. Probabilité que les deux
soient des garçons ? |
Le
deuxième enfant est un garçon ou une fille, indépendamment du premier. La
probabilité est 50%. |
|
|
M. Martin a deux enfants. Au moins un d'eux est un
garçon. Probabilité que les deux
soient des garçons ? |
La
fratrie peut être:
Probabilité
deux garçons: 1 / 3 = 33,3% Voir Les
deux sœurs |
|
|
M. Martin a deux enfants. Au moins un des deux est un
garçon et il est né un lundi. Probabilité que les deux
soient des garçons ? |
La
probabilité est de 48%. La réponse est contre-intuitive et le calcul n'est
pas des plus simples. Voir Solution |
|
|
|
||
|
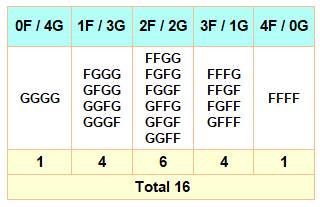
Problème Une famille de quatre enfants. Quelle
est la probabilité d'avoir des enfants de sexes différents:
Autrement-dit:
quelle est la probabilité d'avoir au moins une fille et un garçon ? Solution Sur les 16 possibilités, deux cas pour que des filles
ou que des garçons P (tous filles ou tous garçons) = 2/16 = 1/8 La probabilité d'avoir au moins une fille et un garçon
dans la famille est donc: |
Décompte des
possibilités
Calcul des
probabilités
|
|
Voir Dénombrement
– Index / Probabilités
|
|
||
|
Cas de 1 à 10 enfants Ce tableau montre les situations avec un
exemple. Colonne E: quantité d'enfants dans la
famille. Total: quantité de possibilités pour la
composition de la famille. En haut, est notée la quantité de filles.
La quantité de garçons est le complément pour obtenir la famille. Exemple Avec une famille de 5 enfants, il y a 32
possibilités et, par exemple, 10 cas pour avoir 2 filles et aussi 10 cas pour
avoir 3 filles. Avec 10 cas pour 32 au total, la
probabilité d'avoir 2 filles et 3 garçons (ou l'inverse) est le rapport
10/32, soit 31%. |
Toutes les
possibilités pour les familles de 1 à 10 enfants
Vous
avez reconnu le triangle
de Pascal ? Chaque nombre est égal à la somme de celui du dessus plus son
voisin de gauche. Et
aussi, le total de chaque ligne est une puissance
de 2. |
|
Remarques
|
Il
s'agit de probabilités
!
|
![]()
|
|
|
|
Énigme très classique
et déroutante Anglais: Two boys paradox
/ Boy or Girl paradox Énoncé Dans cette famille, il a deux
enfants. Si je vous apprends qu'il y a une
fille, Quelle est la
probabilité que l'autre soit aussi une fille? Fastoche! Peu importe que l'un soit fille ou garçon,
Tu as raison! Le fait que la famille de
deux enfants ait déjà une fille
D'abord, lorsque la maman est enceinte
Tout faux! Ce n'est pas la bonne
réponse! |
|
![]()
Indice: il n'a jamais été
dit que la fille mentionnée est l'aînée
On lira utilement le Paradoxe de d'Alembert
|
|
|
|
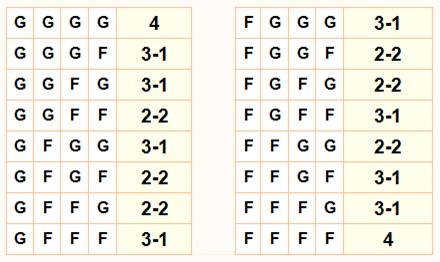
La réponse est 1/3 et non pas ½. Dans cette famille, il
a deux enfants. À ce point de l'énoncé, sans autres
indications, et en tenant compte de l'ordre d'arrivée des enfants, il a
quatre fratries possibles:
Si je vous apprends
qu'il y a une fille, La fratrie 1) "Garçon / Garçon"
n'est pas possible. Il ne reste que trois cas possibles de
fratrie: 2), 3) et 4). Quelle est la
probabilité que l'autre soit aussi une fille? Parmi ces trois fratries, il n'y a qu'une seule possibilité d'avoir
une seconde fille. Il s'agit du cas 4) "Fille /
Fille" Soit, maintenant, un calcul classique de probabilité:
Ici, nous avons un cas favorable (qui
répond à la question) parmi trois possibles. La probabilité est de 1/3 ou 33%. Illustration en tableau G = garçon; F = fille
|
|
|
|
|
|
Une famille de deux enfants:
Probabilité 2/3 ou 66%. |
|
|
|
|||
|
Il s'agit de probabilités
conditionnelles Quelle est la probabilité que A
se produise, sachant que B s'est déjà produit
? |
|||
|
P(A/B) |
=
P(A&B) |
/ P(B) |
|
|
Probabilité de A si B. |
Probabilité d'occurrence de A et aussi de
B. |
Probabilité de B seul. |
|
|
Notre exemple |
|||
|
A
= le
deuxième enfant est une fille |
A&B
= Les deux
enfants sont des filles |
B
= un des
enfants est une fille |
|
|
P(A) = ? |
P(A&B) = 1/4 |
P(B) = 3/4 |
|
|
P(A) = (1/4) / (3/4) = 1/3 |
|||
Voir Nombre
0,333
|
|
||
|
Question Dans une famille de quatre enfants quelle
est la probabilité d'avoir deux filles et deux garçons? Est-ce 50 % ? Non! Réponse: 0,375 = 3/8 Résolution Plus généralement, dans une famille de quatre
enfants quelle est la répartition filles, garçons la plus probable? Notons les
compositions possibles de la famille
Quels sont les cas
possibles?
Dénombrement et calcul
de probabilité
Conclusion Dans une famille de quatre enfants, la plus
grande probabilité est qu'elle soit déséquilibrée avec un seul enfant du même
sexe. Ce n'est pas forcément ce que l'on pense a priori ! |
||
Voir
Nombre
0,375
|
|
|
|
Soit 10 personnes. Chaque année, une meurt
et une vient au monde. Au bout de 10 ans, la probabilité que l'une
d'elles soit vivante est de 34, 868
%. En effet Au bout d'un an, la probabilité est 9/10. Et, pour 10 ans, elle est (9/10)10 =
0,34868. |
|
Voir Probabilité de la vie / Vie
et mort
![]()
|
|
||
|
M. Martin a deux enfants. Au moins un des deux est un garçon et il est né un
lundi. Probabilité que les deux
soient des garçons ? C'est le "au moins" qui change tout" comme pour le paradoxe des deux sœurs. Certains omettent cette mention,
pensant qu'elle est évidente: la famille compte un ou deux garçons. |
La
probabilité est de 48%. La
réponse est contre-intuitive; on s'attend plutôt à 50 % ou alors 33% comme
pour les deux sœurs. Anglais: I have two children. One is a boy born on a Monday.
What is the probability I have two boys? |
|
|
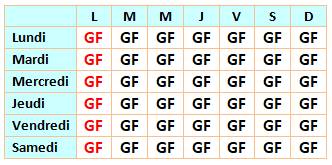
On représente toutes les
possibilités pour le premier enfant en
colonne et celle pour le second en ligne. Soit 49 possibilités. Le cas des deux filles est vite vu, car on nous dit que la
famille compte au moins un garçon. |
|
|
|
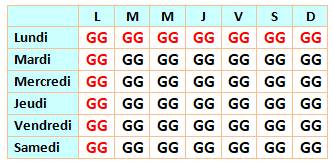
Prenons le cas des deux garçons:
En rouge les 13 cas
possibles. |
|
|
|
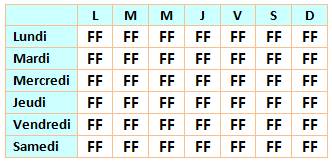
Le premier enfant est un garçon et le second une fille. Cette configuration est
présente 7 fois pour le lundi Nous avons au moins un
garçon, mais ils ne sont pas deux. En rouge, les 7 cas
possibles. |
|
|
|
Le premier enfant est une fille et le second un garçon. Cette configuration est
présente 7 fois pour le lundi Nous avons au moins un
garçon, mais ils ne sont pas deux. En rouge, les 7 cas
possibles. |
|
|
|
Dénombrement: 13 cas favorables (2
garçons) Et 13 + 7 + 7 = 27 cas total
(au moins un garçon). |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()