Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 02/04/2023 M'écrire Brèves de Maths

INDEX Graphe Topologie Dénombrement Logique Jeux	GRAPHES
	Graphe simple	Graphe eulérien	Graphe planaire
	Graphe simple S5	Graphe de Delaunay	Multiple et diviseurs

Faites un double-clic pour un retour en haut de page

GRAPHES SIMPLES à cinq sommets Étude détaillée Comment identifier tous les graphes simples en ne retenant qu'un seul modèle pour toute la série des graphes qui lui ressemblent ? Comment les coder pour un traitement théorique ou informatique ? Recensement de tous les graphes simples à cinq sommets (ils sont 34) avec illustrations de quelques variantes de chaque graphe modèle. Rappel de la quantité de graphes simples: 0, 1, 2, 4, 34, 156, … Illustration: graphe simple à cinq sommets et neuf arêtes
	Sommaire de cette page >>> Les 34 graphes simples à cinq sommets >>> Ressemblance – Isomorphisme >>> Codage des graphes >>> Les 34 graphes un par un	Débutants Dénombrement Glossaire Combinatoire

Les 34 graphes simples à cinq sommets 

Le nombre indique la quantité d'arêtes

Source Image: commons.wikipedia

Ressemblance – Isomorphisme		haut
Graphes isomorphiques Graphes identiques à une rotation près ou une symétrie près. Dans le cas de cet exemple, les quatre graphes sont identiques. Seul un d'entre eux les représente.	Exemple de graphes isomorphiques par rotation de 90°
Autres cas plus délicats D'autres cas se présentent lors de déformations continue du graphe. Autrement-dit par changement de position des sommets tout en gardant les mêmes connexions.	La ressemblance reste assez évidente
Avec ces trois graphes la ressemblance (isomorphisme) est moins évidente. Voir explication ci-dessous	Il est plus difficile d'identifier la ressemblance
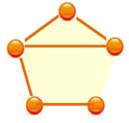
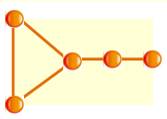
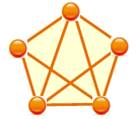
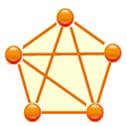
Exemple de transformation Le premier graphe (à gauche) est complet sauf le côté du bas. Les flèches indiquent les déplacements successifs des sommets. Dans le graphe final (à droite), c'est la diagonale supérieure qui manque.

Voir Graphes isomorphes / Autres exemples de graphes isomorphes

Codage des graphes		haut
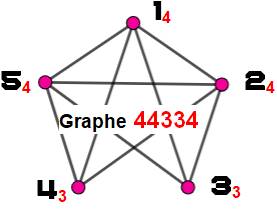
Codage des graphes Le codage est nécessaire pour effectuer des recherches théoriques ou pour exécuter un traitement par ordinateur. On note (rouge) la quantité d'arêtes joignant les sommets numérotés successifs. Ici, un graphe à cinq sommets (5S) et neuf arêtes (9A). Les neufs arêtes imposent que la somme des nombres du codage soit égale à 2 × 9 = 18 = 2S. 4 + 3 + 4 + 4 + 3 = 18. Ce qui veut dire que le codage est une partition du nombre 2S = 18 avec cinq termes chacun ne dépassant pas la valeur 4.	Exemple de codage
, une permutation des nombres engendre un graphe identique. Il suffit de commencer la rotation à partir d'un autre numéro que le 1. Les permutations en 33444 engendrent des graphes isomorphiques pour lesquels c'est un côté qui manque et non une diagonale. Alors, tous ces graphes sont isomorphiques: 33444, 34344, 34434, 34443, 43344, 43434, 43443, 44334, 44343, 44433.	Permutation des nombres du codage
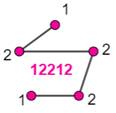
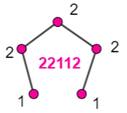
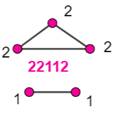
Piège du codage Le graphe-gauche et le graphe-centre ont des codages permutés: 12212 et 22112. Oups ! Avec le même codage, il est possible de créer deux graphes différents: le graphe-centre et le graphe-droite. Pas sympathique pour dénombrer ces graphes!	Bizarreries du codage
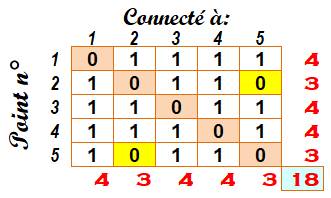
Codage matriciel Chaque ligne représente un point. Chaque colonne indique un point de connexion (1) ou non (0). Évidemment, le sommet k n'est pas connecté au sommet k, car pas de boucle sur lui-même. On retrouve le codage numérique (rouge) en totalisant les "1" sur chaque ligne ou sur chaque colonne. La matrice est symétrique par rapport à la diagonale descendante.	Exemple de codage matriciel

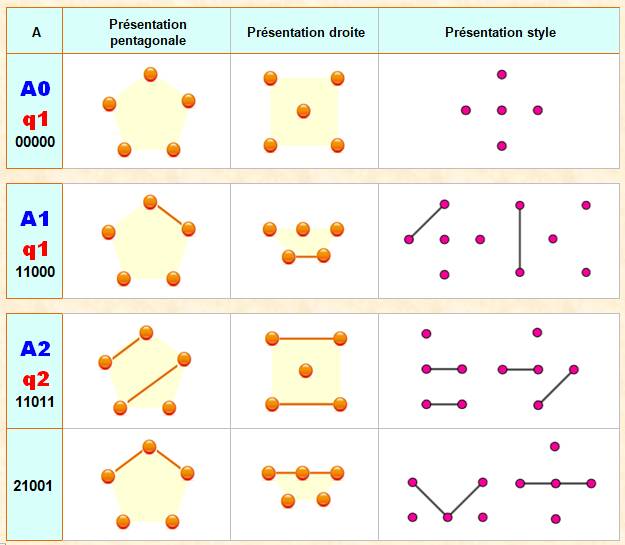
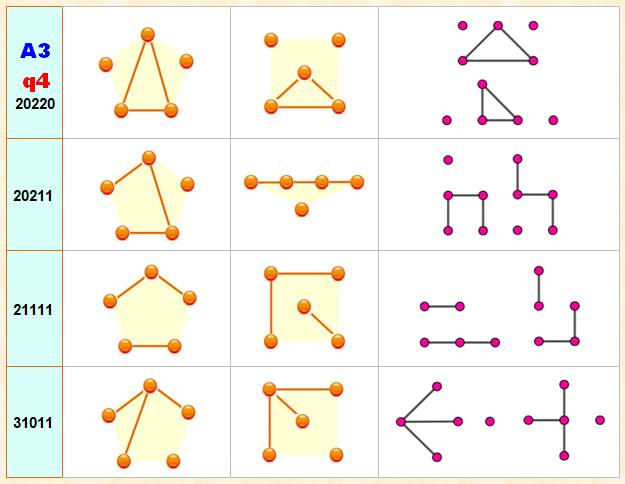
Colonne de gauche: en bleu: quantité d'arêtes de 0 à 10,
en rouge: quantité de graphes pour ce nombre d'arêtes, puis
en noir: le code du graphe.

Puis, trois colonnes avec des variantes pour chaque graphe.

Suite de 0 à 10 sommets en pdf >>>

Haut de page

Retour	GRAPHES SIMPLES Graphe planaire
Suite	Arbres à dénombrement avec nombres de Catalan Arbres de distribution Chemin le plus court Vocabulaire des graphes	Coloration des graphes (nombre chromatique) Graphes et problèmes NP Petit monde Sept amis autour d'une table
Voir	Code Gray Croissance logistique Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index	Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ Trois maisons (énigme des -)
Sites	Simple graph – Wolfram Mathworld OEIS A000088 – Number of graphs on n unlabeled nodes OEIS A086314 – Total number of edges in the distinct simple graphs on n nodes OEIS A001349 – Number of connected graphs with n nodes Types of Graphs with Examples – Geeksforgeeks Autres références générales
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/GrapheS5.htm