Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 02/04/2023 M'écrire Brèves de Maths

INDEX Graphe Topologie Dénombrement	GRAPHES
	Graphe simple	Graphe eulérien	Graphe planaire
	Graphe simple S5	Graphe de Delaunay	Multiple et diviseurs

Faites un double-clic pour un retour en haut de page

GRAPHES SIMPLES Comme leur nom l'indique, ces graphes sont élémentaires, comportant une liaison au maximum entre deux points donnés: une arête au plus entre deux sommets. Un graphe simple est complet si toutes les paires de points sont reliés (Illustration). Le graphe complet à n sommets compte n (n–1) / 2 arêtes.
	Sommaire de cette page >>> Graphes simples >>> Graphes multiples >>> Graphes simples pour n = 1 à 4 >>> Graphes simples – Dénombrement >>> Graphes isomorphes	Débutants Dénombrement Glossaire Combinatoire

Graphe simple – Simple graph or strict graph		haut
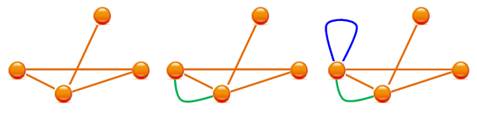
Graphe avec seulement, au plus, une arête entre chaque pair de sommets. Pas de boucles et pas d'arêtes multiples (cas de deux arêtes ou plus connectant deux sommets).	Exemple de graphe simple & contre-exemples sans boucle et avec boucle

Graphe multiple – Multi graph		haut
Graphe avec un nombre quelconque d'arêtes par sommet et qui peut contenir des boucles mais jamais de boucle sur un sommet.	Exemple de graphe multiple

Graphes simples pour n = 1 à 4		haut
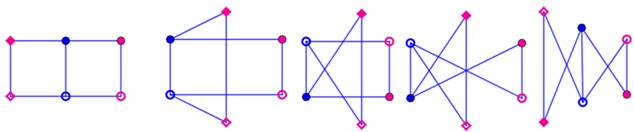
Toutes les possibilités de graphes simples comptant de 0 à n(n–1)/2 arêtes. Pour n = 4, il y a onze graphes simples. En bleu, les deux arbres simples et en vert, le seul graphe complet. On compte 33 arêtes sur l'ensemble de ces graphes.	Onze graphes simples à quatre sommets

Voir Graphes simples à cinq sommets

Graphes simples – Dénombrement		haut
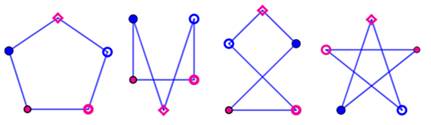
Graphes isomorphiques Graphes identiques à une rotation ou une symétrie près. Dans le cas de cet exemple, les quatre graphes sont identiques. Seul un d'entre eux les représente.	Exemple de graphes isomorphiques par rotation de 90° Voir Autres cas plus délicats avec cinq sommets
Dénombrement à partir de n = 1 Formule pas simple.	1, 2, 4, 11, 34, 156, 1044, 12346, 274668, 12005168, 1018997864, 165091172592, 50502031367952 ...
Quantité total d'arêtes à partir de n = 1	0, 1, 6, 33, 170, 1170, 10962, 172844, 4944024, 270116280, ...

ISOMORPHE

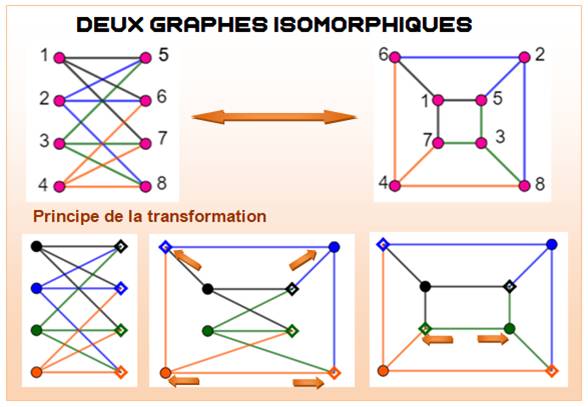
Exemple de graphes isomorphes (non-simples à huit sommets)

Voir Autres cas délicats avec cinq sommets, Autres types de morphismes, Brève 49-975

Autres exemples de graphes isomorphes

Les graphes sur la même ligne sont isomorphes. Les types de sommets aident à imaginer la transformation.

Haut de page

Retour	Graphes – Index Graphe planaire
Suite	Arbres à dénombrement avec nombres de Catalan Arbres de distribution Chemin le plus court Vocabulaire des graphes Coloration des graphes (nombre chromatique) Graphes et problèmes NP Petit monde Sept amis autour d'une table
Voir	Code Gray Croissance logistique Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ Trois maisons (énigme des -)
Sites	Simple graph – Wolfram Mathworld OEIS A000088 – Number of graphs on n unlabeled nodes OEIS A086314 – Total number of edges in the distinct simple graphs on n nodes OEIS A001349 – Number of connected graphs with n nodes Types of Graphs with Examples – Geeksforgeeks Autres références générales
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/GrapheSI.htm