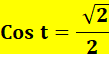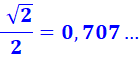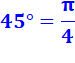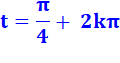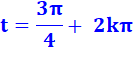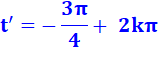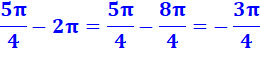|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
TRIGONOMÉTRIE – Cours de Première Mon premier exemple expliqué Je
suis en première. Cette notion de trigonométrie me semble bien étrange! Je souhaite
voir un exemple complètement expliqué pour me familiariser. |
Le cercle trigonométrique
|
ce qu'est le cercle
trigonométrique. Note:
mon expérience me montre que cette révision n'est pas
inutile pour une majorité des personnes de classe de première! |
|
|
||
|
|
Essayer d'apprendre le vélo sans les deux petites roulettes. Pas
facile! Essayer de commencer à peindre sans canevas pour repérer les
proportions; Pas facile! Essayer de construire une maison sans échafaudages. Impossible! En trigo, on utilise le dessin
du cercle trigonométrique. Il a été conçu pour cela! |
|
|
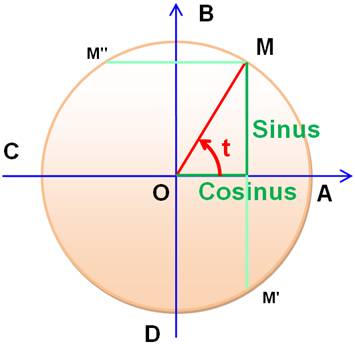
En trigonométrie, "le terrain de jeu" est la circonférence du cercle. Le point M se balade
sur cette circonférence. Les coordonnées du point M s'appellent cosinus et sinus. Ce sont des valeurs qui
caractérisent aussi l'angle
t. Elles prennent des valeurs
exclusivement entre -1 et +1. Une valeur de cosinus caractérise deux points sur le cercle: M et M'. Une valeur de sinus caractérise deux points sur le cercle: M et
M". |
Notez que le cosinus
et à côté de
l'angle. |
|
Familiarisation avec le cercle trigonométrique,
angles et valeurs
|
|
||
|
|
|
|
|
|
Sur l'axe des x, le cosinus vaut:
Je constate que cette valeur est inférieure à 1. c'est compatible avec
un cosinus qui ne doit pas excéder 1. |
|
|
Ou plus exactement en
passant au plus court de |
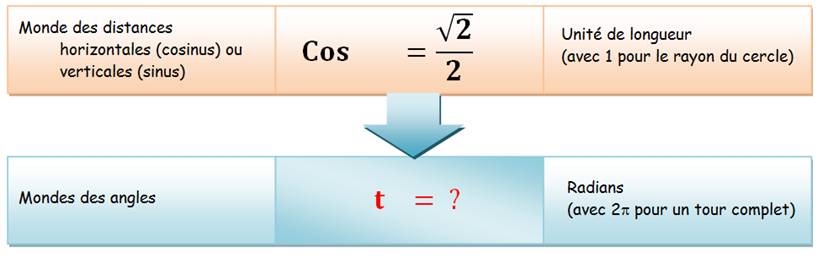
Cette équation conjugue les deux mondes et à nous de retrouver l'angle
inconnu t en connaissant la valeur de son cosinus. |
|
|
|
||
|
|
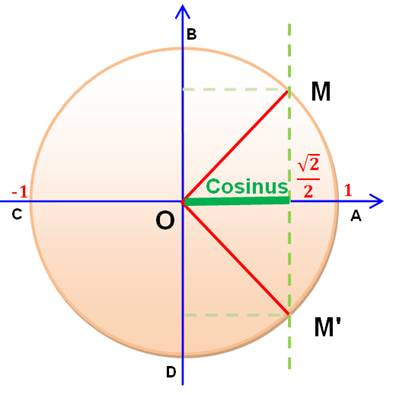
Je pourrais exprimer cette équation d'une autre manière: Quels sont les points M du cercle qui se trouvent à l'abscisse (cosinus):
|
|
|
Mon équation correspond à
deux points (M et M') sur le cercle. Reste à trouver quels sont
les deux angles t et t'. |
|
|
|
|
||
|
On note que
sinus et cosinus = 0,707 forment un carré dont la diagonale fait un angle de
45° avec l'horizontale. |
Je me souviens que cette valeur est au centre de mon tableau et que
cette position centre de symétrie est obtenue pour l'angle de:
|
|
|
|
|
|
|
|
Avec k un nombre entier quelconque, |
|
Rappel de
la table

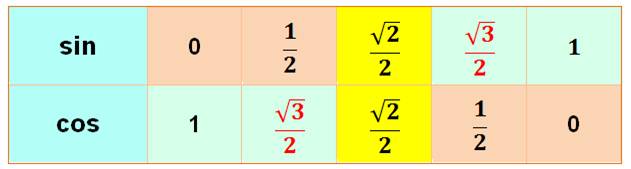
Voir Construction
astucieuse de cette table
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
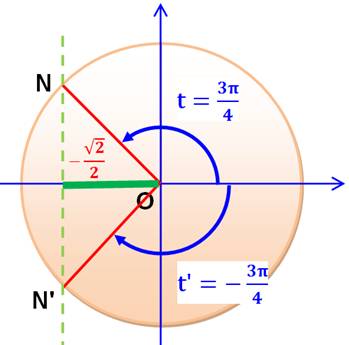
Note sur la valeur de t' En lisant dans le sens
trigonométrique, l'angle t' correspondant au point N' pourrait se lire:
Si à cette valeur, je retire
2k Pi, je retrouve la valeur donnée dans la solution, valeur dite principale.
Les mathématiciens préfèrent
nommer les angles au "plus court", dans le demi-cercle du haut et
dans celui du bas. |
||
Bilan
|
La
résolution d'une équation en trigonométrie consiste à passer du monde des
sinus, cosinus au monde des angles ou inversement. Nous devons savoir
construire la table pour les angles essentiels. La solution passe par la
représentation des données sur le cercle trigonométrique. |
Voir Triangles fous
![]()
|
Suite |
|
|
Bases |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/TrigPrem.htm |
![]()