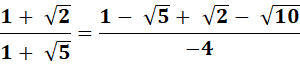|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
TRIGONOMÉTRIE – Cours de Première Revue
des notions étudiées en première. Notions également développées sur d'autres
pages de ce site qui pourront être visitées comme compléments à la
compréhension de ce sujet. Page
réalisée suite à des cours donnés à de jeunes élèves de première. Elle
comprend également quelques rappels de techniques opératoires. |
Le cercle trigonométrique
|
Vous
avez un doute? Vous voulez confirmer votre savoir? N'hésitez pas à revoir
rapidement ce qu'est
le cercle trigonométrique. Note:
mon expérience me montre que cette révision n'est pas
inutile pour une majorité des personnes de classe de première! |
|
|
||
|
Pour l'angle t et pour un cercle de rayon unité:
(c'est l'équivalent de l'abscisse)
(c'est l'équivalent de l'ordonnée)
Sinus² + Cosinus² = 1 |
|
|
Voir Coordonnées / Démonstration de
cette relation sans Pythagore
Doublets cousins
|
Nous
connaissons le doublet abscisse et ordonnée
en géométrie. Nous
avons maintenant le doublet sinus, cosinus
en trigonométrie. Nous
verrons le doublet réel, imaginaire en
algèbre des nombres complexes. Dans
les trois cas, nous caractérisons un point M du plan avec deux nombres. Dans
le cas des nombres complexes (notés: a + ib),
a et b sont des nombres réels et i est un symbole représentant la
racine carrée imaginaire de – 1. Une belle
astuce qui va se révéler payante pour simplifier de nombreux calculs de
trigonométrie, notamment en électronique. |
|
|
||
|
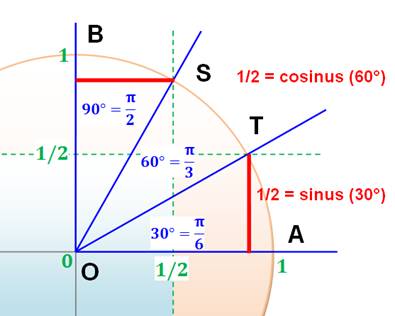
Remarques importantes
cos de 60° =
sinus 30° = 1/2 En
remarquant que 30° = 90° – 60° |
Je me familiarise avec les radians
|
|
Voir Constructions géométriques
élémentaires
|
|
||
|
OA = OS = AS = 1
|
SH² + OH² = OS² = 1 SH² = 1 – (1/2)² = 1 – 1/4 = 3/ 4
|
|
|
|
||
|
|
SH² + OH² = OS² = 1 2 SH² = 1
|
|
Technique de calcul avec les racines carrées
|
Deux
racines Tout
d'abord, on n'oublie pas qu'un carré est le produit de
deux nombres positifs ou de deux nombres négatifs. 2
x 2 = 4 et ( – 2) x ( – 2) = 4 Cela est vrai, à
l'envers, pour les racines
carrées: un nombre entier positif possède deux
racines carrées:
Pas de
racine au dénominateur, si c'est possible On
cherche toujours à éliminer les racines au dénominateur. C'est
plus facile à visualiser et plus facile à traiter.
Si
la racine est accompagnée d'une constante, alors il faut utiliser la fraction
unitaire formée du conjugué. Voir exercice ci – dessous. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Diviser un angle
|
Pi/2
divisé par 3 donne Pi/6. Je le constate bien sur une figure. Attention
pour le calculer! Ne pas appliquer "sauvagement" la règle qui dit
que je multiplie par l'inverse de 3.
Le
3 sous la barre de fraction est un nombre entier et non une fraction. Pour
devenir une fraction, il faut écrire 3/1, et son inverse
est 1/3.
On
aurait tout aussi bien pu dire: je prends le tiers de Pi/2:
|
|
|
|
|
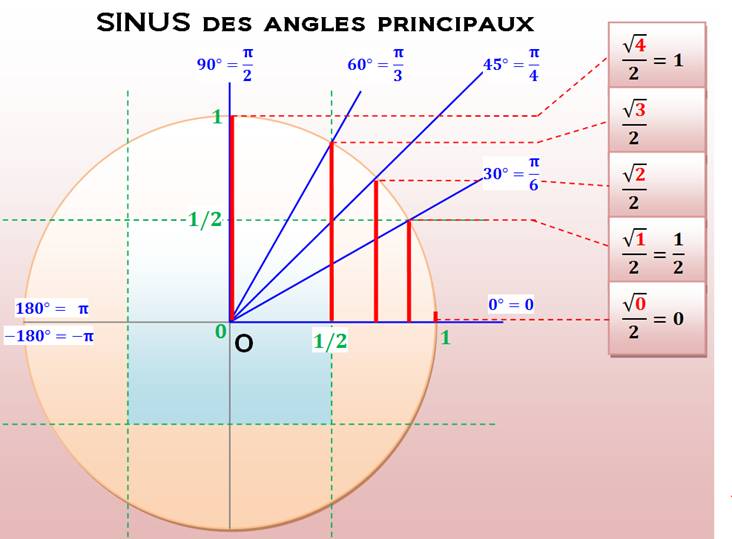
Pour mémoriser ce tableau:
Se souvenir de la technique
opératoire avec les racines:
|
|
Pour info: rectangle trigonométrique

Voir Brève 910
|
|
|
|
Exemples L'angle 3Pi/2 est
manifestement
|
|
Modulo enroulé
|
Imaginez
un vélodrome avec un anneau de 250 m de long. Ce cycliste sait qu'en dix
minutes il fait toujours un peu plus de vingt tours, mais il veut comparer ses
records. Tous les jours, lorsque le chrono marque 10 minutes, il note de
combien il dépasse: 55 m puis 78 m et aujourd'hui, c'est 105 m. Il vient de
battre son record! Ce
cycliste fait un calcul en modulo sans le
savoir. En
trigonométrie, seul l'angle sur le cercle compte. Le nombre tours que
pourrait faire cet angle ne nous intéresse pas. Il peut tourner cent fois,
mille fois … on s'en fiche! On
dit que l'angle est connu à 2k |
|
Voir Les modulos quotidiens avec
l'heure
|
|
|
|
Exemple: le sinus de l'angle en 1 est égal au sinus de l'angle en 4; égal aussi
à l'opposé du sinus de l'angle en 8 …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Illustration
|
|
Voir Fonctionnement de la radio – Diaporama
Junior
|
|
||
|
|
Pas de relation évidente entre les longueurs des
traits rouges et verts. |
|
Voir Autres formules de ce genre
![]()
|
Suite |
|
|
Bases |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/TrigPrem.htm |
![]()