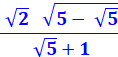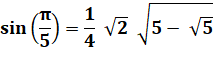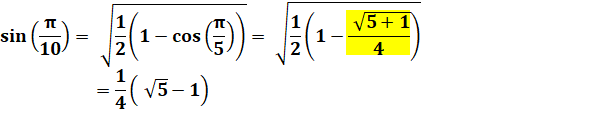|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
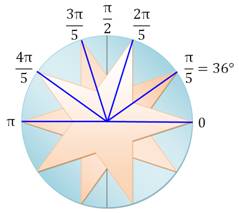
TRIGONOMÉTRIE Calcul des lignes
trigonométriques de l'angle 36° = Pi/5 Angle
caractéristique de l'étoile à cinq branches. |
Approximations
|
|
sin 36° = cos 54° |
= 0,587785252… |
|
10 / 17 |
= 0,588235294… |
|
|
Écart |
= 0,000450042… |
|
|
|
tan 72° |
= 3,077683543… |
|
tan 71,56505…° |
= 3 |
|
|
Écart |
= 0,435 …° |
Voir Construction
approchée du pentagone avec 10/17 et
avec arctan(3)

Voir Nombre d'or = 2 x 0,8090 … = 1,
618 …
![]()
![]()
|
|
|
|
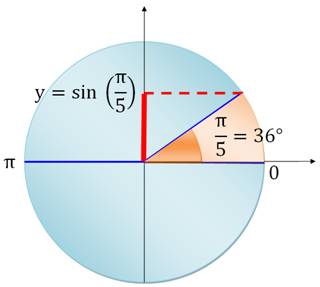
sin Pi/4 = sin(45°) =
0,707 … = sin Pi/5 = sin(36°) = 0,587 … sin Pi/6 = sin(30°) = 0,5
|
|
|
|
||
|
|
|
|
|
|
||
|
|
sin (5x) = 16A5 – 20A3 + 5A avec A = sin(x) |
|
|
|
sin (5 ( = 16A5 – 20A3 + 5A avec A = sin( |
|
|
|
16A5 – 20A3 + 5A = 0 A (16A4 – 20A2 + 5) = 0 16A4 – 20A2 + 5 = 0 Avec B = A² 16B2 – 20B + 5 = 0 |
|
|
|
||
|
|
ax² + bx + c = 0
|
|
|
|
ax² + bx + c = 0 16B2 – 20B + 5 = 0 a = 16, b= –20 et c = 5
|
|
|
|
A1 = 0,901 … (signe plus) A2 = 0,587 … (signe moins)
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Valeur avec 100
décimales
|
Sinus 0, 5877852522 9247312916 8705954639
0727685976 5243764314
5991072272 4807572784 7416235195
7508504049 8627413360 … Cosinus 0, 8090169943 7494742410
2293417182 8190588601 5458990288
1431067724 3113526302
3140945122 4853603602 0946955688 … Tangente 0, 7265425280 0536088589
5466757480 6187496160 9239296520 8462750066 3273457493
9184568308 8420577522 2161400914 … |
Voir Racine de 5
![]()
|
|
|
|
Calculs des sinus (les cosinus et
tangentes s'en déduisent)
Comment calculer cette valeur?
Voir Formule
trigo en quintuple / Résolution
équation du second degré Résolution
en x²
En
comparant à l'ordre de grandeur cherché => c'est le signe moins qui
convient.
Voir sin²
+ cos² = 1
Voir Formules
de l'angle moitié
|
|
Voir Calculs
pour Pi / 8 / Icosagone
![]()
|
Rappel |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()