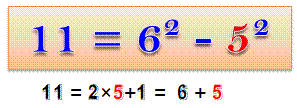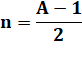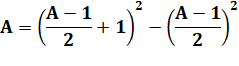|
|||||||||||||||||||||||||||||||||
![]()
|
Nombres IMPAIRS / PAIRS & CARRÉS Propriétés simples et magiques!
Explication: (k + 1)² – k² = k² +
2k + 1 – k² = 2k + 1 Motif
semblable avec les multiples de 4:
|
Voir Factorisation de Fermat / Machine à factoriser
de Carissan
Démonstration muette pour les impairs
Voir Différence
de carrés
|
|
|
|
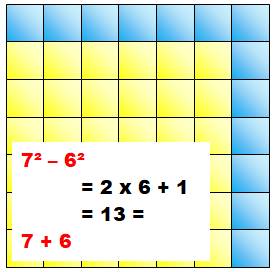
Principe
On considère les deux nombres x et x+1. Leur somme donne n. La différence de leur carré donne aussi n. |
|
|
n+1
n somme (n+1)² n² différence 2 1 3 4 1 3 3 2 5 9 4 5 4 3 7 16 9 7 5 4 9 25 16 9 6 5 11 36 25 11 7 6 13 49 36 13 8 7 15 64 49 15 9 8 17 81 64 17 10 9 19 100 81 19 11 10 21 121 100 21 12 11 23 144 121 23 13 12 25 169 144 25 14 13 27 196 169 27 15 14 29 225 196 29 16 15 31 256 225 31 17 16 33 289 256 33 18 17 35 324 289 35 19 18 37 361 324 37 20 19 39 400 361 39 21 20 41 441 400 41 22 21 43 484 441 43 23 22 45 529 484 45 24 23 47 576 529 47 25 24 49 625 576 49 26 25 51 676 625 51 27 26 53 729 676 53 28 27 55 784 729 55 29 28 57 841 784 57 30 29 59 900 841 59 31 30 61 961 900 61 32 31 63 1 024 961 63 33 32 65 1 089 1 024 65 34 33 67 1 156 1 089 67 35 34 69 1 225 1 156 69 36 35 71 1 296 1 225 71 37 36 73 1 369 1 296 73 38 37 75 1 444 1 369 75 39 38 77 1 521 1 444 77 40 39 79 1 600 1 521 79 41 40 81 1 681 1 600 81 42 41 83 1 764 1 681 83 43 42 85 1 849 1 764 85 44 43 87 1 936 1 849 87 45 44 89 2 025 1 936 89 46 45 91 2 116 2 025 91 47 46 93 2 209 2 116 93 48 47 95 2 304 2 209 95 49 48 97 2 401 2 304 97 50 49 99 2 500 2 401 99 |
|
|
||
|
|
n + (n+1) = 2n + 1 (n+1)² – n² = n² + 2n + 1
– n² = 2n + 1 (n + 1)² – n² = (n+1-n) (n+1+n) = 2n + 1 |
|
|
Démonstration |
|
|
|
|
A = 2n + 1 A = 2n + 1 + n² – n²
= (n + 1)² – n²
|
|
|
|
||
|
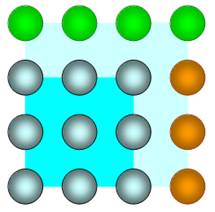
En
ajoutant d'abord une ligne de 4, puis une colonne de 3. (n + 1)² = n² + (n +
1) + n Gd
carré = Pt Carré + n + n + 1 La partie ajoutée (2n = 1) pour
passer d'un carré au suivant est appelée le gnomon. |
|
|
|
Pourquoi
ne pas imposer que la partie ajoutée, le gnomon, soit aussi un nombre carré?
5² - 4² = 5 + 4 = 9
= 3² ou 4² + 3² = 5² |
|
|
|
|
|||
|
|
100 100 |
= 99 + 1 =
101 – 1 |
|
|
|
100 100 |
=
50² – 49² + 1 =
51² – 50² – 1 |
|
|
On
obtient une expression pour le double du nombre pair considéré. |
200 |
=
51² - 49² |
|
|
Ces
deux nombres sont de part et d'autre du quart de n. |
100 8 12 |
=
26² – 24 ² = 3² –
1² = 4² –
2² |
|
|
|
|
|
Sont différences de
deux carrés les: -
Nombres impairs n = 2k + 1 = (k+1)² - k² -
Nombres divisibles par 4: n = 4 k = (k+1)² - (k-1)² Quant aux nombres
pairs: n = 2 k =
(k+1)² – k² - 1 (formule
des impairs avec le 1 qui a changé de côté). |
|
Curiosités, quel que soit n
|
(n + 1)² – (n –
1)² = 4n (n + 2)² – (n –
2)² = 8n (n + 3)² – (n –
3)² = 12n |
n = 100 101² – 99² = 400 102² – 98² = 800 103² – 97² = 1200 |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()