|
||||||||||||||||||||||||||||
![]()
|
ÉCART entre CARRÉS de nombres consécutifs ou proches Théorème qui dit que tout
nombre est atteint de façon unique
par le carré d'un nombre n et adition ou soustraction d'un nombre inférieur
ou égal à n >>> Puis, quelques propriétés et curiosités avec les carrés
des nombres et leurs différences >>> Relations entre carrés d'un nombre et carré des nombres
inférieurs de même parité >>> Calcul mental des carrés >>> |
|
On
connait 25 = 5² et 36 = 6²dont les chiffres du second sont ceux du premier plus un. Trouvez d'autres tels couples. |
Somme de deux carrés consécutifs
|
Propriété a²
+ (a + 1)² = 2a² + 2a + 1 = 2a (a + 1) + 1 La
somme des carrés de deux nombres consécutifs
est égale à deux fois leur produit plus 1. Exemples: 20² + 21² = 2 x 20 x 21 + 1 = 841 = 29² (triplet de Pythagore)
10² + 11² = 2 x 10 x 11 +
1 = 221 = 14,866 …² |
![]()
|
|
|||
|
On
appelle couverture numérique d'un carré
toute la plage de nombres autour de n² plus ou moins tous les nombres jusqu'à
n. Donc de n² – n à N² + n. L'empan d'un carré est constitué des deux nombres
bornant la plage. |
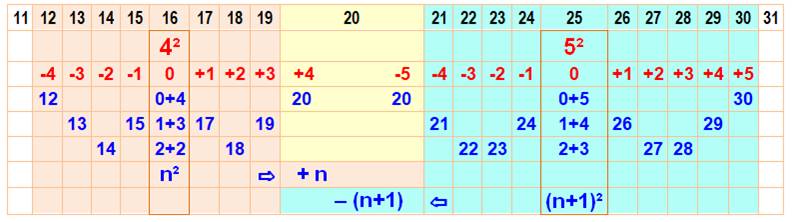
Couverture numérique de 4² 12, 13, 14, 15, 16, 17, 18, 19, 20 Empan de 4² {12, 20} Couverture numérique de 5² 20, 21, 22, 23, 24, 25, 26, 27, 28, 29,
30 Empan de 4² {20, 30} |
||
|
Couverture numérique des
carrés successifs
Les carrés couvrent tous les nombres
une seule fois, sauf doublon aux extrémités. Le doublon des extrémités s'explique: (n+1)² –
(n+1) = n² + 2n + 1 – n – 1 = n² + n Exemple en tableau La première ligne est la suite des
nombre incluant les deux carrés successifs 16 et 25. La troisième ligne note les écarts
par rapport à ces carrés. Ex: 12 est à -4 de 4² et 20 à +4 de
4², comme à -5 de 5². En bas, on note que 20 est à n de n²
et à (n+1) de (n+1)²
Dans l'encadré, on donne les
partitions du nombre porté au carré. |
|||
|
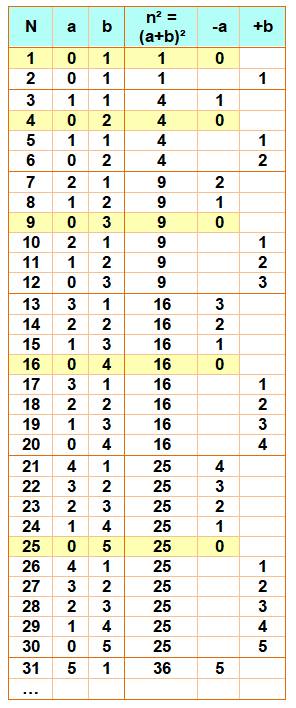
Exemple pour les nombres de 1
à 31 L'algorithme
de création de ce tableau est le
suivant:
(a + b)² + b = N
On
constate que:
Formalisation Tous les
nombres entiers positifs sont atteints une seule fois par la formule (a + b)²
– a ou la formule (a + b) + b. Ou
encore: Théorème Pour tout nombre entier N non nul, il existe
un couple de nombres entiers (a, b) unique
avec b non nul, tel que N = (a + b)² – a ou N
= (a + b)² + b Exemples 123 = (2 + 9)² + 2 = 11² + 2 1 234 = (9 + 26)² + 9 = 35² + 9 12 345 =
(24 + 87)² + 24 = 111² + 24 321 = (3 + 15)² – 15 = 18² – 3 4 321 = (31 + 35)² – 35 = 66² – 35 54 321 =
(32 + 201)² + 32 = 233² + 32 |
|
||
![]()
|
|
||
|
|
||
|
Exemples |
13² = 10² + 3 x
23 = 100 + 69
= 169 57² = 50² + 7 x 107 = 2 500 + 749 =
3 249 48² = 50² – 2 x
98 = 2 500 – 200 + 4 = 2 304 |
|
|
Identité
remarquable |
|
|
|
Exemples |
4 = 4 x 1
x 1 = (1 + 1)² – (1 – 1)² = 2² 8 = 4 x 2
x 1 = (2 + 1)² – ( 2 – 1)² = 3² – 1² 12 = 4 x 3 x 1 = (3 + 1)² – ( 3 – 1)² = 4² – 2² 16 = 4 x 4 x 1 = (4 + 1)² – ( 4 – 1)² = 5² – 3² 32 = 4 x 4 x 2 = (4 + 2)² – ( 4 – 2)² = 6² – 2² 48 = 4 x 4 x 3 = (4 + 3)² – ( 4 – 3)² = 7² – 1² |
|
|
|
|
|
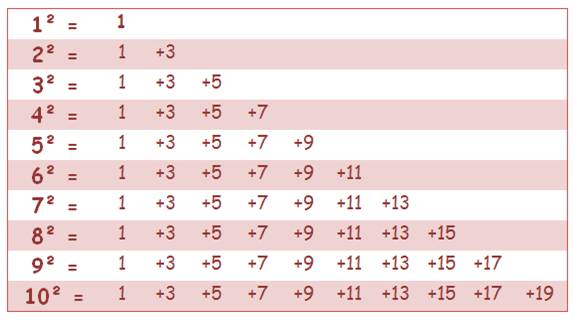
Observons la progression des carrés: l'écart entre un
carré et le suivant; de même que le différentiel entre ces écarts:
Voir Machine de Babbage / Somme de carrés
(démonstration) La différence entre
les carrés de deux nombres consécutifs
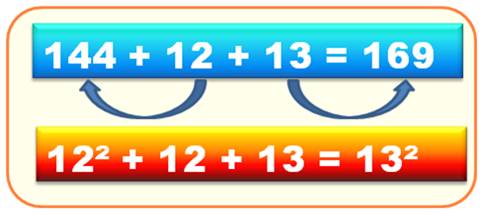
est égale au double du plus petit nombre augmenté de 1. La différence s'exprime également comme la somme des
deux nombres consécutifs concernés. Ex:
5² + 5 + 6
= 6² Tout nombre impair est la différence
des carrés de deux nombres consécutifs: N =
2k – 1 = k² – (k – 1)² . Voir Nombres impairs
|
|
Voir Découverte
Junior du calcul mental des carrés (fichier .ppt)
/ Différence
de deux carrés
|
|
|
|
Ces constats découlent directement de la formulation de
la différence entre deux carrés de nombres consécutifs. (n + 1)² – n² =
2n + 1 Ex: 11 = 2x5 + 1 = 6² – 5² 21 = 2x10 + 1 =
11² – 10² 101 = 2 x 50 + 1 = 51² – 50² Réciproquement 101² – 100² = 2 x 100 + 1 =
201 9² –
8² = 2 x 8 + 1 = 17 On
rappelle Tout nombre
impair est la différence
des carrés de deux nombres consécutifs. Autre écriture symétrique: n² + n = (n + 1)² – (n + 1) Ex: 10² + 10 = 11² – 11 Formule qui peut être utilisée sans connaître le
moindre carré: Ex: 1234² + 1234 = 1235² – 1235 |
|
Voir Carré des nombres en 999…
|
|
|||||||||
|
Deux nombres entiers consécutifs ont pour carrés 633
616 et 635 209. Comment trouver facilement le carré du nombre entier
suivant? Solution
|
|||||||||
|
|
|
|
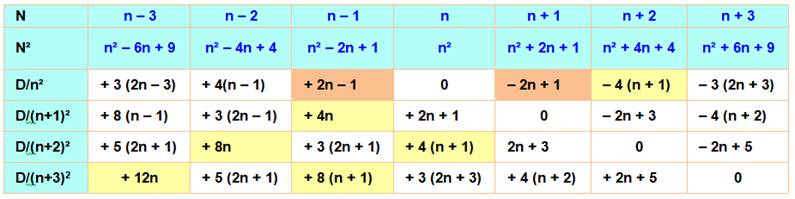
Comment
passer d'un carré à ses voisins immédiats ou un peu plus lointains? Ce
tableau montre les écarts entre carrés de n – 3 à n + 3. D/n² veut
dire: quelle est la quantité à ajouter pour atteindre la valeur 0 de la même
ligne. Exemple de lecture pour passer de (n – 3)² à n², il faut ajouter 3 (2n – 3). Exemple numérique: n = 8, 5² = 25
et 8² = 25 + 3 (2x8 – 3) = 25 + 39 = 64
En
marron, le cas de l'écart unité traité ci-dessus. En jaune,
cas simples, propices au calcul mental. Exemple: connaissant 10² =
100, calculez 16². Alors, n = 13 et 16² = 100 + 12 x 13 = 100 + 120
+ 36 = 256. La
formule générale est la suivante: (n + k)² – (n +
h)² = 2 (k – h) n + k² – h² Exemple: pour k = 5 et h
= –3: (n + 5)² – (n – 3)² = 2 x 8 n + 25 – 9 = 16n + 16 = 16 (n + 1) Si n = 10: 15²
– 7² = 16 x 11 = 176; en effet:
225 – 49 = 176. On note
en particulier la diagonale descendante en 4n, 8n, 12n … qui conduit à la
formule: (n + k)² – (n –
k)² = 4 k n Exemple: pour un écart de
10: k = 5 Alors, 22² + 12² = 4 x 5 x 10 = 200; en effet:
484 – 144 = 200. Voir Divisibilité par 4 / Divisibilité par 8 Exemple de stratégie possible pour
calculer mentalement les carrés On s'appuie sur un carré proche connu (50). Calculer l'écart (13) et prendre la partie paire
(12) plus un éventuellement La valeur de k est la moitié de l'écart pair (6).
La suite est montrée sur cette illustration.
|
|
Voir Calcul
mental – Index
Voir Somme des impairs –
démo / Impairs, Carrés et Cubes
|
|
|
|
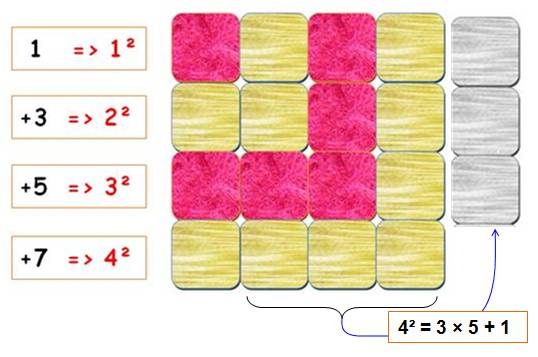
L'ajout d'une équerre – un nombre impair – suffit à conserver le carré en forme comme en nombre. Notez que: carré
= somme des impairs successifs: 1 + 3 + 5 + 7 + … + (2n – 1) = n² Autre propriété des carrés: carré =
produit des voisins plus un n² = (n – 1) (n + 1) + 1 |
|
Voir Gnomon / Somme des
impairs
|
|
||
|
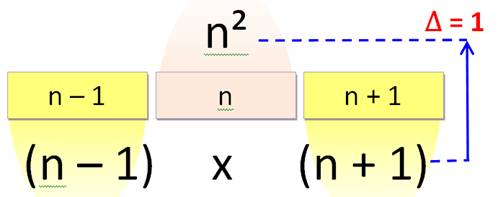
Un carré moins le produit des nombres adjacents est égal à 1. Évident d'après cette identité remarquable: (n – 1)(n+1) = n² – 1 |
|
|
|
|
||
Voir Application au
calcul du produit de deux nombres distants de 2
|
|
||
|
Avec
cette identité remarquable, il est possible de relier tout carré à tous les
carrés inférieurs de même parité |
|
|
|
Carré de nombres pairs 64 = 8² = 6² + 28 = (7 + 1)² =
(7 – 1)² + 4 x (7 x 1) = 4² + 48 = (6 +
2)² = (6 – 2)² + 4 x (6 x 2) = 2² + 60 = (5 +
3)² = (5 – 3)² + 4 x (5 x 3) = 0² + 64 = (4 +
4)² = (4 – 4)² + 4 x (4 x 4) Carré de nombres impairs 81 = 9² = 7² + 32 = (8 + 1)² =
(8 – 1)² + 4 x (8 x 1) = 5² + 56 = (7 +
2)² = (7 – 2)² + 4 x (7 x 2) = 3² + 72 = (6 +
3)² = (6 – 3)² + 4 x (6 x 3) = 1² + 80 = (5 +
4)² = (5 – 4)² + 4 x (5 x 4) Le carré d'un nombre est égal au carré de tous les nombres inférieurs
de même parité augmenté de quatre fois le produit des deux nombres mis au
carré. |
||
Voir Problème de Viète
|
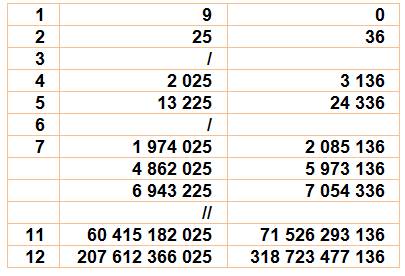
Table des carrés à chiffres incrémentés Une exploration
systématique donne ce tableau Par exemple
pour 4 chiffres: 2 025 = 45² et 3 136 = 56²; les deux carrés ayant des
chiffres incrémentés (+1).
Note: pas de
propagation de retenue 9 devient 0. D'où le premier cas trivial. Avec propagation de
retenue, pour trois chiffres, on aurait 289 et 400 Recherche raisonnée Par contre, il est
possible de chercher par raisonnement. Par exemple pour 5 chiffres: En effet m² – n²= (m +
n) (m – n) = 11 111 = 41 x 271 = 1 x 11 111 Si m – n = 41 => n
= m – 41 => m + n = 2m – 41 =
271 => m = 156 et n = 115 => m² = 24 336 et n² = 13 225 Si m – n = 1 => n =
m – 1 => m + n = 2m – 1 = 11
111 => m = 5 556 non car six
chiffres. La solution est
unique. Avec des chiffres augmentés de 2, le premier exemple: 1
969 850 689, 3 181 072 801 Avec des cubes: seule solution 8 et 9. |
![]()
|
Suite |
|
|
Débutants |
|
|
Voir |
|
|
Cette page |
![]()