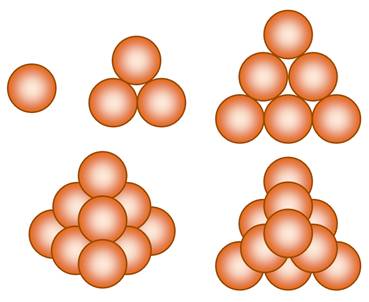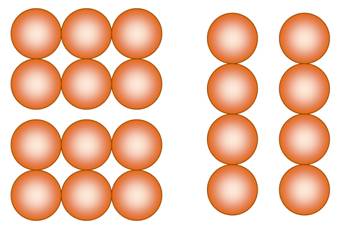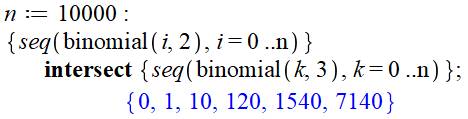|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES TÉTRAÉDRIQUES ou Nombre pyramide à base
triangulaire Nombres figurés associés au tétraèdre. Formés par la somme des nombres
triangulaires. Nombres de la forme: Tn =
1/6 n (n + 1) ( n + 2) Le sixième du produit de trois
nombres consécutifs. Les nombres tétraédriques sont en
troisième position dans le triangle
de Pascal. |
Anglais: Tetrahedral
numbers or triangular pyramidal numbers
|
|
|
|
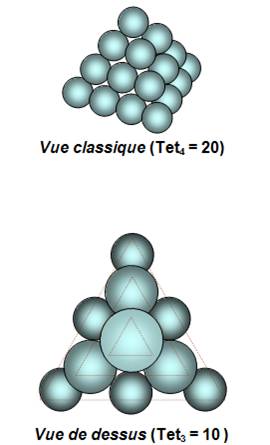
Les
trois rangées de 1, 3 et 6 boules (en
haut) se superposent pour donner une pile pyramidale de 10 boules (en bas).
Vue de profil et vue de dessus. C'est
la disposition des fruits (pommes, pèches …) que l'on trouver sur un étal de
maraîcher. |
|

20 = 1 + 3 +
6 + 10
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
20 = 1 + 3 + 6 + 10
20 = 10 + 10 35 = 20 + 15
|
Cette vue montre un
empilement de triangles:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Liste des nombres tétraèdres: 0, 1, 4, 10, 20, 35, 56, 84, 120,
165, 220, 286, 364, 455, 560, 680, 816, 969, 1140, 1330, 1540, 1771, 2024,
2300, 2600, 2925, 3276, 3654, 4060, 4495, 4960, 5456, 5984, 6545, 7140, 7770,
8436, 9139, 9880, 10660, 11480, 12341, 13244, 14190, 15180 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Les nombres triangulaires sont en deuxième
position dans le triangle
de Pascal et les tétraédriques en troisième position. Il est facile d'écrire un programme qui recherche
les nombres communs. soit, les nombres qui sont à la fois (intersect) dans la
liste (séquence) des triangulaires (binomial, 2) et dans celle des
tétraédriques (binomial, 3):
Suite en Produits
de consécutifs
Tous ces nombres figurent dans la cinquième diagonale du triangle de Pascal. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Pyramide
triangle / Nombre
140
|
|
|||||||||||||||||||||||||||||||||||||||
|
Formule de calcul |
Tetn
= 1/6 n (n + 1) (n + 2) |
||||||||||||||||||||||||||||||||||||||
|
Conséquences
|
Tout produit de trois nombres consécutifs
est divisible par 6. |
||||||||||||||||||||||||||||||||||||||
|
Table de
multiplication
Exemple: 10 = 3 + 4 + 3
Tet4 = 20 = 2 (4 +
6) = 2 (1x4 +
2x3) = 1x4 +
2x3 + 3x2 + 4x1 |
|
||||||||||||||||||||||||||||||||||||||
|
Forme générale
|
Tetn = n + 2(n – 1) + 3(n – 2)
+ ... (n – 2)3 + (n – 1)2 + n Tet5
= 1x5 + 2x4 + 3x3 + 4x2 + 5x1 = 35 |
||||||||||||||||||||||||||||||||||||||
|
Conséquence |
Les
tétraédriques sont pairs sauf 1 sur 5 (ceux qui se terminent par 5) 1 4 10 20 35 56 84 120 165 |
||||||||||||||||||||||||||||||||||||||
|
Triangle de Pascal |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
123321 4567654 … 17 x 18 x 19 /6 = 969 |
|||||||||||||||||||||||||
|
palindrome
tétraèdre connu. |
|
|||||||||||||||||||||||||
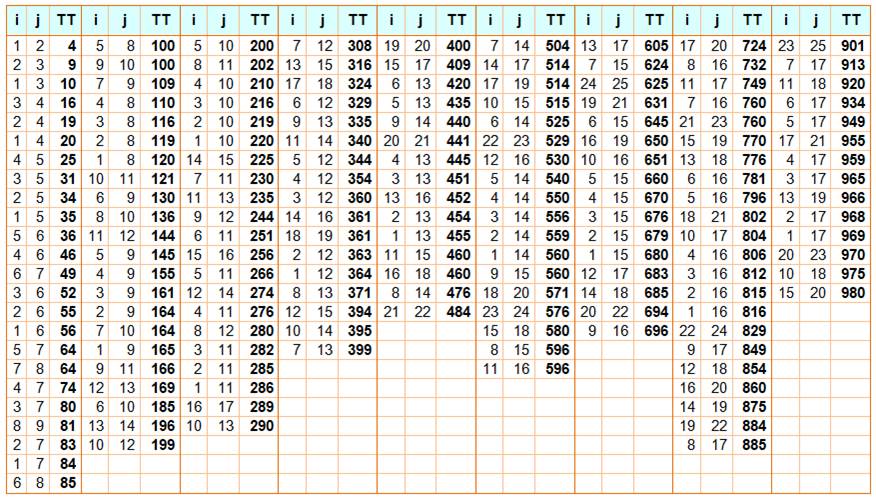
Table des nombres pseudo-tétraédriques (TT), somme des triangulaires de
i à j
TT24 =
Triangulaire 2 + Triangulaire 3 + Triangulaire
4 = 3 + 6 + 10 = 19
|
Valeurs suivantes de TT: 1020, 1024,
1044, 1054, 1055, 1056, 1060, 1084, 1085, 1089, 1091, 1105, 1110, 1120, 1130,
1135, 1136, 1139, 1140, 1154, 1156, 1160, 1165, 1176, 1208, 1210, 1211, 1219,
1225, 1246, 1252, 1254, 1270, 1274, 1295, 1296, 1306, 1310, 1316, 1320, 1326,
1329, 1330, 1331, 1344, 1354, 1369, 1375, 1385, 1396, 1407, 1420, 1444, 1456,
1460, 1464, 1484, 1485, 1489, 1505, 1520, 1521, 1530, 1536, 1539, 1540, 1551,
1569, 1570, 1585, 1595, 1600, 1606, 1620, 1630, 1631, 1651, 1660, 1681, 1684,
1687, 1715, 1736, 1738, 1740, 1751, 1760, 1761, 1764, 1767, 1770, 1771, 1784,
1785, 1786, 1802, 1804, 1845, 1849, 1859, 1883, 1891, 1895, 1904, 1920, 1924,
1936, 1940, 1946, 1956, 1968, 1989, 1999, 2004, 2014, 2020, 2023, 2024, 2025,
2035, 2036, 2040, 2050, 2080, 2109, 2110, 2114, 2116, 2135, 2136, 2145, 2180,
2195, 2209, 2216, 2224, 2236, 2244, 2245, 2265, 2280, 2289, 2290, 2296, 2299,
2300, 2304, 2307, 2314, 2324, 2330, 2341, 2360, 2365, 2380, 2401, 2435, 2452,
2460, 2461, 2470, 2471, 2480, 2485 … |
![]()
|
Nombres géométriques |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()