|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
EN BREF –
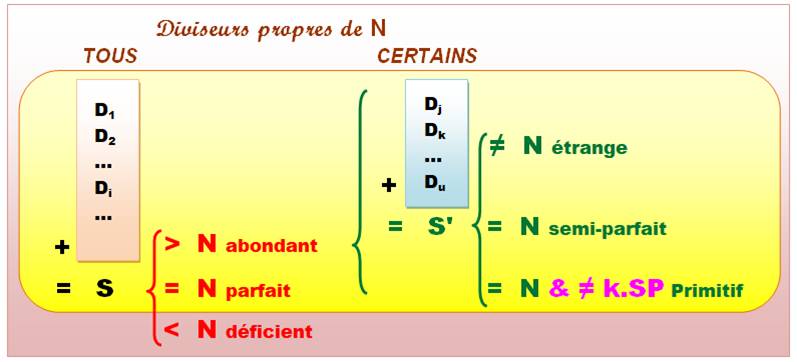
Place et nomenclature des nombres semi-parfaits
Les nombres
semi-parfaits (ou pseudo-parfaits) sont tous abondants (on admet les parfaits
parmi eux).
Les abondants non
semi-parfaits sont dits étranges.
Les semi-parfaits
irréductibles sont primitifs.
Voir Analyse des
semi-parfaits et du produit
correspondant des diviseurs
![]()
|
Approche |
|
|
|
Définitions |
Nombre
parfait:
il est égal à la somme de ses diviseurs propres (tous les diviseurs sauf
lui-même) Nombre
semi-parfait
(ou pseudo-parfait): il est égal à la somme de certains de ses diviseurs
propres; souvent plusieurs fois. |
|
|
Exemples |
Diviseurs de 12: 1,
2, 3, 4, 6 et 12 = 6 + 4 + 2 =
6 + 3 + 2 + 1 |
Diviseurs de 18: 1,
2, 3, 6, 9 et 18 = 9 + 6 + 3 = 9 + 6 + 2 + 1 |
Voir Introduction et place des
semi-parfaits
|
Général |
Un
nombre semi-parfait (SP) est toujours abondant
ou parfait. Un
nombre abondant non-SP est un nombre
étrange (weird number). Un
multiple de SP est un SP. Tous
les nombres en 6 k sont SP. Les
nombres en 2m p avec p premier impair et p < 2m – 1
sont SP. Notamment avec p = 2m+1 – 1, un premier
de Mersenne. Tout
nombre pratique, non puissance de 2, est SP. |
|
Primitif |
Un
SP non divisible par un SP plus petit est primitif.
Soit: un SP dont aucun de ses diviseurs n'est lui-même SP. Exemples: 6, 20, 28, 104, 272 … |
|
Anglais |
Semiperfect
numbers or pseudoperfect numbers A semiperfect number
is a natural number that is equal to the sum of all or some of its proper
divisors. A primitive
pseudoperfect number is a pseudoperfect number that is not a multiple of any
other pseudoperfect number. |
|
|
|
|
Liste des 247 nombres semi-parfaits
inférieurs à 1001 Les trois nombres en rouge sont parfaits 6, 12, 18, 20, 24, 28,
30, 36, 40, 42, 48, 54, 56, 60, 66, 72, 78, 80, 84, 88, 90, 96, 100, 102, 104,
108, 112, 114, 120, 126, 132, 138, 140, 144, 150, 156, 160, 162, 168, 174,
176, 180, 186, 192, 196, 198, 200, 204, 208, 210, 216, 220, 222, 224, 228,
234, 240, 246, 252, 258, 260, 264, 270, 272, 276, 280, 282, 288, 294, 300,
304, 306, 308, 312, 318, 320, 324, 330, 336, 340, 342, 348, 350, 352, 354,
360, 364, 366, 368, 372, 378, 380, 384, 390, 392, 396, 400, 402, 408, 414,
416, 420, 426, 432, 438, 440, 444, 448, 450, 456, 460, 462, 464, 468, 474,
476, 480, 486, 490, 492, 496, 498, 500, 504, 510, 516, 520, 522, 528,
532, 534, 540, 544, 546, 550, 552, 558, 560, 564, 570, 572, 576, 580, 582,
588, 594, 600, 606, 608, 612, 616, 618, 620, 624, 630, 636, 640, 642, 644,
648, 650, 654, 660, 666, 672, 678, 680, 684, 690, 696, 700, 702, 704, 708,
714, 720, 726, 728, 732, 736, 738, 740, 744, 748, 750, 756, 760, 762, 768,
770, 774, 780, 784, 786, 792, 798, 800, 804, 810, 812, 816, 820, 822, 828,
832, 834, 840, 846, 852, 858, 860, 864, 868, 870, 876, 880, 882, 888, 894,
896, 900, 906, 910, 912, 918, 920, 924, 928, 930, 936, 940, 942, 945, 948, 952, 954,
960, 966, 968, 972, 978, 980, 984, 990, 992, 996, 1000. Semi-parfaits impairs 945 est le plus petit
semi-parfait impair. Les suivants: 1575, 2205, 2835, 3465, 4095, 4725, 5355, 5775,
5985, 6435, 6615, 6825, 7245, 7425, 7875, 8085, 8415, 8505, 8925, 9135 … Semi-parfaits primitifs 6,
20, 28, 88, 104, 272, 304, 350, 368, 464, 490, 496, 550, 572, 650, 748, 770,
910, 945, 1184,
1190, 1312, 1330, 1376, 1430, 1504, 1575, 1610, 1696, 1870, 1888, 1952, 2002,
2170, 2205, 2210, 2470, 2530, 2584, 2590, 2870, 2990, 3010 … Voir Nombres abondants primitifs |
|
|
|
|||
|
6, {1, 2, 3} 12, {2, 4, 6} 12, {1, 2, 3, 6} 18, {3, 6, 9} 18, {1, 2, 6, 9} 20, {1, 4, 5, 10} 24,
{4, 8, 12} 6 24,
{1, 3, 8, 12} 24,
{2, 4, 6, 12} 24,
{1, 2, 3, 6, 12} 24,
{1, 2, 3, 4, 6, 8} 28, {1, 2, 4, 7, 14} 30, {5, 10, 15} 30, {2, 3, 10, 15} 30, {1, 3, 5, 6, 15} 36,
{6, 12, 18} 7 36,
{2, 4, 12, 18} 36,
{3, 6, 9, 18} 36,
{1, 2, 3, 12, 18} 36,
{1, 2, 6, 9, 18} 36,
{2, 3, 4, 9, 18} 36,
{2, 3, 4, 6, 9, 12} 40, {2, 8, 10, 20} 40, {1, 4, 5, 10, 20} 40, {1, 2, 4, 5, 8, 20} 42, {7, 14, 21} 42, {1, 6, 14, 21} 48,
{8, 16, 24} 10 48,
{2, 6, 16, 24} 48,
{4, 8, 12, 24} 48,
{1, 3, 4, 16, 24} 48,
{1, 3, 8, 12, 24} 48,
{2, 4, 6, 12, 24} 48,
{1, 2, 3, 6, 12, 24} 48,
{2, 4, 6, 8, 12, 16} 48,
{1, 2, 3, 4, 6, 8, 24} 48,
{1, 2, 3, 6, 8, 12, 16} 54, {9, 18, 27} 54, {3, 6, 18, 27} 54, {1, 2, 6, 18, 27} 56, {2, 4, 8, 14, 28} 56, {1, 2, 4, 7, 14, 28} 60,
{10, 20, 30} 34 60,
{3, 12, 15, 30} 60,
{4, 6, 20, 30} 60,
{5, 10, 15, 30} 60,
{1, 2, 12, 15, 30} 60,
{1, 3, 6, 20, 30} 60,
{1, 4, 5, 20, 30} 60,
{1, 4, 10, 15, 30} 60,
{2, 3, 5, 20, 30} 60,
{2, 3, 10, 15, 30} 60,
{2, 6, 10, 12, 30} 60,
{3, 5, 10, 12, 30} 60,
{3, 10, 12, 15, 20} 60,
{4, 5, 6, 15, 30} 60,
{1, 2, 3, 4, 20, 30} 60,
{1, 2, 5, 10, 12, 30} 60,
{1, 2, 10, 12, 15, 20} 60,
{1, 3, 4, 10, 12, 30} 60,
{1, 3, 5, 6, 15, 30} 60,
{2, 3, 4, 6, 15, 30} 60,
{2, 5, 6, 12, 15, 20} |
60,
{3, 4, 5, 6, 12, 30} 60,
{3, 4, 6, 12, 15, 20} 60,
{4, 5, 6, 10, 15, 20} 60,
{1, 2, 3, 4, 5, 15, 30} 60,
{1, 2, 4, 5, 6, 12, 30} 60,
{1, 2, 4, 6, 12, 15, 20} 60,
{1, 3, 4, 5, 12, 15, 20} 60,
{1, 3, 5, 6, 10, 15, 20} 60,
{2, 3, 4, 5, 6, 10, 30} 60,
{2, 3, 4, 6, 10, 15, 20} 60,
{3, 4, 5, 6, 10, 12, 20} 60,
{1, 2, 3, 4, 5, 10, 15, 20} 60,
{1, 2, 4, 5, 6, 10, 12, 20} 66, {11, 22, 33} 66, {2, 3, 6, 22, 33} 72,
{12, 24, 36} 31 72,
{3, 9, 24, 36} 72,
{4, 8, 24, 36} 72,
{6, 12, 18, 36} 72,
{1, 2, 9, 24, 36} 72,
{1, 3, 8, 24, 36} 72,
{1, 8, 9, 18, 36} 72,
{2, 4, 6, 24, 36} 72,
{2, 4, 12, 18, 36} 72,
{3, 6, 9, 18, 36} 72,
{4, 6, 8, 18, 36} 72,
{1, 2, 3, 6, 24, 36} 72,
{1, 2, 3, 12, 18, 36} 72,
{1, 2, 6, 9, 18, 36} 72,
{1, 3, 6, 8, 18, 36} 72,
{1, 6, 8, 9, 12, 36} 72,
{1, 8, 9, 12, 18, 24} 72,
{2, 3, 4, 9, 18, 36} 72,
{3, 4, 8, 9, 12, 36} 72,
{3, 6, 9, 12, 18, 24} 72,
{4, 6, 8, 12, 18, 24} 72,
{1, 2, 3, 4, 8, 18, 36} 72,
{1, 2, 4, 8, 9, 12, 36} 72,
{1, 2, 6, 9, 12, 18, 24} 72,
{1, 3, 6, 8, 12, 18, 24} 72,
{2, 3, 4, 6, 9, 12, 36} 72,
{2, 3, 4, 9, 12, 18, 24} 72,
{3, 4, 6, 8, 9, 18, 24} 72,
{1, 2, 3, 4, 6, 8, 12, 36} 72,
{1, 2, 3, 4, 8, 12, 18, 24} 72,
{1, 2, 4, 6, 8, 9, 18, 24} 78, {13, 26, 39} 80, {4, 16, 20, 40} 80, {2, 8, 10, 20, 40} 80, {1, 4, 5, 10, 20, 40} 80, {1, 5, 8, 10, 16, 40} 80, {2, 4, 8, 10, 16, 40} 80, {1, 2, 4, 5, 8, 20, 40} 84,
{14, 28, 42} 25 84,
{2, 12, 28, 42} 84,
{7, 14, 21, 42} 84,
{1, 6, 7, 28, 42} 84,
{1, 6, 14, 21, 42} 84,
{2, 7, 12, 21, 42} 84,
{3, 4, 7, 28, 42} 84,
{3, 4, 14, 21, 42} 84,
{3, 6, 12, 21, 42} 84,
{1, 2, 4, 7, 28, 42} |
84,
{1, 2, 4, 14, 21, 42} 84,
{1, 2, 6, 12, 21, 42} 84,
{1, 3, 4, 6, 28, 42} 84,
{2, 3, 4, 12, 21, 42} 84,
{2, 7, 12, 14, 21, 28} 84,
{3, 6, 7, 12, 14, 42} 84,
{3, 6, 12, 14, 21, 28} 84,
{1, 2, 6, 7, 12, 14, 42} 84,
{1, 2, 6, 12, 14, 21, 28} 84,
{1, 3, 4, 6, 7, 21, 42} 84,
{2, 3, 4, 7, 12, 14, 42} 84,
{2, 3, 4, 12, 14, 21, 28} 84,
{1, 2, 3, 4, 6, 12, 14, 42} 84,
{1, 3, 4, 6, 7, 14, 21, 28} 84,
{1, 2, 3, 4, 6, 7, 12, 21, 28} 88, {1, 2, 8, 11, 22, 44} 90,
{15, 30, 45} 23 90,
{5, 10, 30, 45} 90,
{6, 9, 30, 45} 90,
{1, 5, 9, 30, 45} 90,
{2, 3, 10, 30, 45} 90,
{2, 10, 15, 18, 45} 90,
{3, 9, 15, 18, 45} 90,
{1, 2, 3, 9, 30, 45} 90,
{1, 2, 9, 15, 18, 45} 90,
{1, 3, 5, 6, 30, 45} 90,
{1, 5, 6, 15, 18, 45} 90,
{2, 6, 9, 10, 18, 45} 90,
{3, 5, 9, 10, 18, 45} 90,
{5, 6, 9, 10, 15, 45} 90,
{1, 2, 3, 6, 15, 18, 45} 90,
{1, 2, 5, 9, 10, 18, 45} 90,
{2, 3, 6, 9, 10, 15, 45} 90,
{2, 6, 9, 10, 15, 18, 30} 90,
{3, 5, 9, 10, 15, 18, 30} 90,
{1, 2, 3, 5, 6, 10, 18, 45} 90,
{1, 2, 3, 5, 9, 10, 15, 45} 90,
{1, 2, 5, 9, 10, 15, 18, 30} 90,
{1, 2, 3, 5, 6, 10, 15, 18, 30} 96,
{16, 32, 48} 21 96,
{4, 12, 32, 48} 96,
{8, 16, 24, 48} 96,
{1, 3, 12, 32, 48} 96,
{2, 6, 8, 32, 48} 96,
{2, 6, 16, 24, 48} 96,
{4, 8, 12, 24, 48} 96,
{1, 3, 4, 8, 32, 48} 96,
{1, 3, 4, 16, 24, 48} 96,
{1, 3, 8, 12, 24, 48} 96,
{2, 4, 6, 12, 24, 48} 96,
{4, 8, 12, 16, 24, 32} 96,
{1, 2, 3, 4, 6, 32, 48} 96,
{1, 2, 3, 6, 12, 24, 48} 96,
{1, 3, 8, 12, 16, 24, 32} 96,
{2, 4, 6, 8, 12, 16, 48} 96,
{2, 4, 6, 12, 16, 24, 32} 96,
{1, 2, 3, 4, 6, 8, 24, 48} 96,
{1, 2, 3, 6, 8, 12, 16, 48} 96,
{1, 2, 3, 6, 12, 16, 24, 32} 96,
{1, 2, 3, 4, 6, 8, 16, 24, 32} 100,
{5, 20, 25, 50} 100,
{1, 4, 20, 25, 50} |
|
|
Liste des quantités de sommes des SP jusqu'à 500 En rouge les records de quantités [6, 1],
[12, 2], [18, 2], [20, 1], [24, 5], [28, 1], [30, 3], [36, 7], [40, 3], [42,
2], [48, 10], [54, 3], [56, 2], [60, 34], [66, 2], [72, 31], [78, 1], [80, 6], [84, 25],
[88, 1], [90, 23], [96, 21], [100, 2], [102, 1], [104, 1], [108, 20], [112,
4], [114, 1], [120, 278], [126, 13], [132,
15], [138, 1], [140, 15], [144, 116], [150, 9], [156, 11], [160, 12], [162,
4], [168, 197], [174, 1], [176, 2], [180, 751],
[186, 1], [192, 42], [196, 2], [198, 9], [200, 12], [204, 6], [208, 2], [210,
151], [216, 169], [220, 7], [222, 1], [224, 9], [228, 8], [234, 6], [240, 2157], [246, 1], [252, 516], [258, 1], [260, 6],
[264, 121], [270, 130], [272, 1], [276, 6], [280, 119], [282, 1], [288, 469],
[294, 4], [300, 446], [304, 1], [306, 4], [308, 6], [312, 106], [318, 1],
[320, 25], [324, 54], [330, 93], [336, 1554], [340, 4], [342, 5], [348, 2],
[350, 3], [352, 5], [354, 1], [360, 22208],
[364, 5], [366, 1], [368, 1], [372, 2], [378, 75], [380, 3], [384, 85], [390,
75], [392, 6], [396, 344], [400, 44], [402, 1], [408, 79], [414, 3], [416,
4], [420, 19244], [426, 1], [432, 1246], [438, 1], [440, 76], [444, 2], [448,
18], [450, 289], [456, 67], [460, 2], [462, 54], [464, 1], [468, 269], [474,
1], [476, 4], [480, 17049], [486, 5], [490, 1], [492, 2], [496, 1], [498, 1],
[500, 3]. Liste des records de
quantité de sommes des SP jusqu'à 720 [6, 1], [12, 2], [24, 5], [36, 7],
[48, 10], [60, 34], [120, 278], [180, 751], [240, 2157], [360, 22208], [720,
676327] |
|||
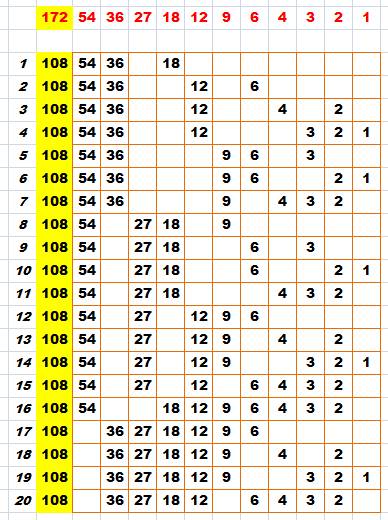
Analyse du nombre 108:
20 fois sommes de certains de ses diviseurs propres
Premier
nombre: le diviseur utilisé pour réaliser la somme;
le second nombre: le reste à ajouter pour atteindre 108.

Voir DicoNombre: Nombre 108
|
|
||
|
Un
tableur est particulièrement approprié pour effectuer la recherche des sommes
possibles Les
diviseurs sont affichés (en rouge) avec leur somme (172, le nombre 108 est abondant). Mode opératoire Une colonne est réservée au calcul de la somme. Chaque ligne correspond à un essai pour réaliser
la somme avec les diviseurs de poids décroissants. La somme est ajustée pour atteindre 108 en
abandonnant les diviseurs qui font dépasser cette valeur. |
|
|
|
|
||
|
|
Informations générales L'instruction divisors(n)
produit l'ensemble des diviseurs de n; avec minus on lui retire le nombre n. Note: les
accolades spécifient un ensemble et
non une liste. L'instruction minus nécessite aussi un ensemble d'où n entre
accolades. |
|
|
|
L'instruction subsets
engendre tous
les sous-ensembles de l'ensemble des diviseurs (en bleu à droite du
programme). Pratique pour analyser toutes les combinaisons
possibles des élément de l'ensemble par 2, par 3 etc. nextvalue et finished sont deux instructions propres au
traitement de sous-ensembles >>> |
|
|
|
Détection des semi-parfaits Commentaire Appel des deux packages de logiciels: combinatoire
et théorie des nombres. Déclaration de la procédure SP (semi-parfait).
Déclaration des paramètres propres à la procédure (local). La variable oui fait l'hypothèse a priori que n
n'est pas un nombre semi-premier. Création des sous ensembles de diviseurs propres
en S. Boucle avec écriture propre à l'analyse des
sous-ensembles. La somme (convert
+) des éléments de chaque sous-ensemble
est placée en a. Si cette somme a est égale à n alors n est un
nombre semi-parfait (oui = true). Arrêt de
la recherche (break) La valeur de oui est rendue visible à l'extérieur
(return). Fin de procédure. Programme principal définissant n. Déclaration d'une liste vide pour y loger les n
semi-parfaits. Boucle d'analyse de n de 1 à 100 (par exemple). Si SP(n) retourne une valeur vraie (true) alors le nombre n est ajouté à la liste. Fin de condition (fi)
et fin de boucle (od). Impression de la liste L (lprint). Résultat en bleu. |
|
|
with(combinat): with(numtheory): SP := proc (n) local
SS, S, a, oui; oui := false; SS := `minus`(divisors(n), {n}); S :=
subsets(SS); while not S[finished] do a := convert(S[nextvalue](), `+`); if a
= n then oui := true; break end if end do; return oui end proc; L := []; for
n from 1 to 100 do if `and`(SP(n) = true, `mod`(n, 2) = 1) then L := [op(L),
n] end if end do; lprint(L): |
|
|
|
|
Sommes des semi-parfaits Commentaire Même type de programme (sans procédure) Dans la boucle d'analyse des sommes de diviseurs:
La différence par rapport au programme précédent:
on poursuit les recherches jusqu'à épuisement des sous-ensembles. On les
imprime au fur et mesure de leur découverte. En bleu, impression des 20 sommes trouvées. Quantité confirmé par le compte fait à l'aide du
compteur kt. |
![]()
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPDIVIS/Semiparf.htm |
![]()