|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Définition |
Nombre
pratique ou nombre panarithmique : nombre entier tel qu'il est possible de
construire tous les nombres inférieurs avec la somme
de certains de ses diviseurs. Un diviseur n'est utilisé qu'une seule
fois. Un
entier positif m est pratique si tout n compris entre 1 et m, inclus, est la
somme de diviseurs distincts de m. |
|
Exemples |
Pour
certains nombres, il existe plusieurs choix pour effectuer la somme. C'est
celle qui a le moins de termes qui est préférée (pas le cas sur ces tableaux
où on a choisi la somme des plus petits nombres). |
Voir Introduction et place des
semi-parfaits
|
Général |
Définition
proposée en 1948 par A.K. Srinivasan. Les
nombres pratiques permettent la "pesée"
des nombres plus petits avec les diviseurs, d'où le nom de nombres pratiques. Les
sommes des diviseurs d'un nombre pratique atteignent tous les nombres jusqu'à
la somme de tous les diviseurs. Ex: avec les diviseurs propres de 12 (somme
16), on peut former tous les nombres de 1 à 16. En
ajoutant n, on atteint tout les nombres jusqu'à la somme complète des
diviseurs (soit: 28 pour n = 12) Les
nombres pratiques sont tous pairs. Alors
que 10 n'est pas pratique, 100 et 1000 le sont. Tous
les nombres parfaits
sont pratiques. Les
nombres en 2n-1 (22 – 1) sont pratiques pour n > 1. Tout
entier positif est la somme de deux nombre pratiques. G. Melfi. Il
existe une infinité de nombres pratiques en
m – 2 , m et m + 2. G. Melfi. |
|
Comme Goldbach |
Tout nombre pair est la somme de deux nombres pratiques. Théorème
démontré en 1996 alors que la conjecture de
Goldbach avec les nombres premiers n'est toujours pas résolue. |
|
Quantité |
En
2015, Weingartner a montré que la quantité de nombres pratiques inférieurs à
n est de l'ordre de:
Avec
pi(x), la quantité
de nombres premiers inférieurs à x et c une constante, sans doute proche
de 1,341. Les
deux fonctions se "rejoignent" à l'infini (le rapport entre les
deux tend vers 0 lorsque x tend vers l'infini). |
|
Caractérisation (Steward et Sierpinski) |
Soit
un nombre n >1. Sa
factorisation: La
somme des diviseurs: Alors,
le nombre est pratique si: pour
j de 2 à k. |
|
f-pratique |
Les
nombres f-pratiques sont la généralisation des nombres pratiques en
additionnant des fonctions des diviseurs propres. Nicholas Schwab, Lola
Thompson (2017). |
|
Anglais |
Practical
numbers A practical number is a positive integer n such that all smaller
positive integers can be represented as sums of distinct divisors of n.
Divisors are not repeated in the sum. |
Voir Nombres
idonéaux (Convenient numbers)
|
|
|
|
1,
2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64,
66, 72, 78, 80, 84, 88, 90, 96, 100, 104, 108, 112, 120, 126, 128, 132, 140,
144, 150, 156, 160, 162, 168, 176, 180, 192, 196, 198, 200, 204, 208, 210,
216, 220, 224, 228, 234, 240, 252, 256, 260, 264, 270, 272, 276, 280, 288,
294, 300, 304, 306, 308, 312, 320, 324, 330, 336, 340, 342, 348, 352, 360,
364, 368, 378, 380, 384, 390, 392, 396, 400, 408, 414, 416, 420, 432, 440,
448, 450, 456, 460, 462, 464, 468, 476, 480, 486, 496, 500, 504, 510, 512,
520, 522, 528, 532, 540, 544, 546, 552, 558, 560, 570, 576, 580, 588, 594,
600, 608, 612, 616, 620, 624, 630, 640, 644, 648, 660, 666, 672, 680, 684,
690, 696, 700, 702, 704, 714, 720, 726, 728, 736, 740, 744, 750, 756, 760,
768, 780, 784, 792, 798, 800, 810, 812, 816, 820, 828, 832, 840, 858, 860,
864, 868, 870, 880, 882, 888, 896, 900, 912, 918, 920, 924, 928, 930, 936,
952, 960, 966, 968, 972, 980, 984, 990, 992, 1000. |
|
Le nombre
200 est un nombre pratique:
tous les nombres jusqu'à 200
peuvent être exprimés
par une somme de ses diviseurs.
Sur ce tableau, la plus
petite possibilité.

|
|
||
|
Instructions utilisées et leurs
effets
|
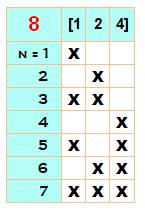
Explications Avec divisors(n),
on obtient l'ensemble des diviseurs de 4. Avec choose,
on forme la liste L de toutes les combinaisons des diviseurs de 4. L'indice i = 8 demande à considérer le 8e
élément de la liste L, qui est lui-même une liste: [1,2,4]. Avec nops(L[i]),
on obtient la quantité d'éléments (jmax = 3). Avec add de j à
jmax, on additionne tous les éléments: 1 + 2 + 4 = 7. |
|
|
Procédure et programme
|
Commentaires Ouverture des packages numtheory
et combinat pour disposer des instruction divisors et choose. La procédure PR teste si le nombre n est
pratique. La combinaison des diviseurs est placée dans la
liste L. On ouvre une liste M destinée à recevoir les
sommes de diviseurs. La boucle en i analyse chaque combinaison de
diviseurs. La liste M est remplie avec les sommes (add)
successives des diviseurs. La boucle en j examine tous les nombres
inférieurs à n. L'indicateur oui est placé à 0 (n n'est pas pratique par
défaut). La boucle en i balaie toutes les sommes de
diviseurs trouvées et les compare à j. Si il y a correspondance (i = j),
l'indicateur oui est mis à 1 et passage à la suite (break). Cette boucle terminée, si oui = 0 (pas de
correspondance), passage au nombre j suivant (sortie de la boucle en j). Si l'indicateur est à 1 alors on transmet n vers
la sortie. Le programme principal examine en séquence les
nombres n de 1 à 30. |
|
|
with(numtheory): with(combinat):
PR := proc (n) local L, M, i, j, oui; L := choose([op(divisors(n))]); M := [];
for i to nops(L) do M := [op(M), add(L[i][j], j = 1 .. nops(L[i]))] end do;
for j from 0 to n-1 do oui := 0; for i in M do if i = j then oui := 1; break
end if end do; if oui = 0 then break end if end do; if oui = 1 then n end if
end proc: seq(PR(k), k = 1 .. 30); |
Listing du programme |
|
Voir Programmation – Index
![]()
|
Voir |
|
|
Sites |
|
|
Cette
page |
http://villemin.gerard.free.fr/aNombre/TYPDIVIS/Pratique.htm |
![]()