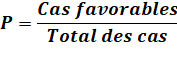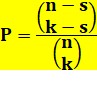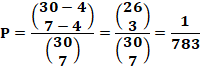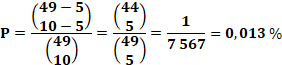|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Tirage de boules façon LOTO avec grilles multi-jeux TIRAGE (n, k, s)
Exemple avec le cas (10, 3, 2)
But Quelle est la probabilité de
gagner avec une grille ? |
|
|
||||
|
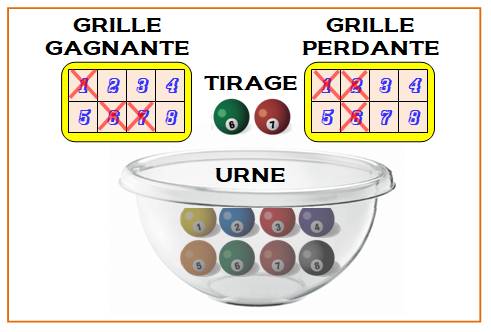
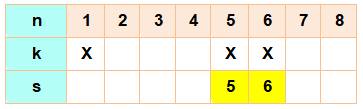
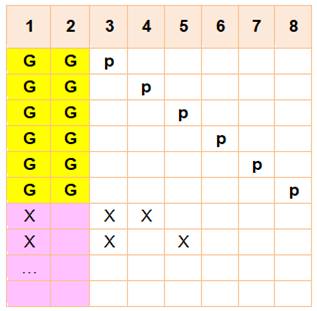
Cas: 8, 3, 2 Il s'agit
d'un tirage parmi n = 8 boules. Deux
boules gagnantes: 5 et 6. Un
ticket-grille où on peut cocher 3 numéros. Ici: 1, 5 et 6, c'est gagné ! D'une manière
générale, quelle est la probabilité de gagner avec un ticket 3-grille ? |
Jeu (8, 3, 2)
Trois numéros cochés, dont les deux sortis: le ticket est gagnant. Notez que l'ordre des numéros est sans importance. |
|||
|
Ce qu'il
faut trouver:
La probabilité
de gain est le rapport entre les deux quantités. |
|
|||
|
Commentaire Supposons
que ce soit une forme de loto. Il y a
des gens qui jouent avec des grilles à deux numéros ou trois numéros ou k
numéros. D'une
part, le prix du ticket-grille sera de plus en plus élevé, mais c'est le
problème des joueurs; et, D'autre
part, il pourra y avoir des gagnants multiples sur un type ou l'autre de
grilles, mais c'est le problème de l'organisateur des jeux de repartir les
gains. |
Ce qui nous intéresse, ce n'est pas le gain
escompté, mais la probabilité de gagner avec une grille de trois numéros à
cocher pour deux numéros gagnants. Dans ce monde des 3-grilles, prenons autant de joueurs que nécessaire pour que chacun
joue une grille différente. Il en faut autant que de combinaisons de 3 parmi 8, soit 56 joueurs. Leur probabilité de gagner est de 100%. Parmi eux, certains vont avoir coché les deux
bons numéros. Ils sont 6 gagnants. Il y a sans doute d'autres gagnants avec
d'autres grilles, mais ce n'est pas notre problème. La probabilité de gain de chaque 3-grille est
donc: P = 6/56 = 10,7%. |
|||
Une petite familiarisation avant d'aborder le cas général.
|
|
||
|
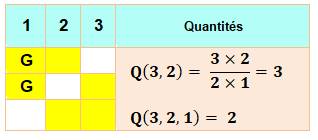
Cas: 3, 2, 1 Cas de
trois boules et une boule gagnante (disons
la n°1). Le raisonnement serait le même avec l'une des autres boules.
|
Q(3, 2) = quantité de combinaisons de 2 parmi 3. Q(3, 2, 1) = quantité de possibilités pour gagner avec une grille à deux
numéros. |
|
|
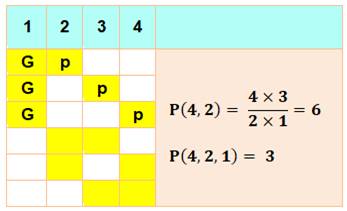
Cas: 4, 2, 1 Cas de
quatre boules et une boule gagnante (disons la n°1).
Notez que si c'est un
autre numéro de boule qui est gagnant, il a tout autant de possibilités. Il y
a bien trois cases jaunes dans chaque colonne. |
En considérant les trois grilles gagnantes, remarquez que le deuxième
numéro coché (p) correspond à un choix de 1 parmi 3, un des trois numéros
perdants. |
|
|
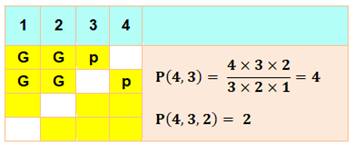
Cas: 4, 3, 2 Cas de quatre
boules et deux boules gagnantes (disons la n°1 et la n°2).
|
En terme de dénombrement, deux étapes de raisonnement:
En disant cela, on signifie qu'il y a seulement deux possibilités pour
avoir les deux tickets gagnants. |
|
![]()
|
Avec des grilles à cocher donnant
la possibilité de couvrir plusieurs combinaisons de jeux à la fois, on
démultiplie la possibilité de gain dans la proportion donnée par la formule. Dans le cas (49, 10, 5) la
probabilité de gagner avec un ticket est voisine de 1 sur 2 millions; avec
une 10-grille, elle est de 1 sur 7 567. La société des jeux doit sans doute
la faire payer cher ! Rappel important: la probabilité annonce une moyenne sur une très grande
quantité de jeux. Même avec 7 567 fois une 10-grille, on n'est toujours pas
sûr de gagner. Une question se pose: combine de grilles faut-il jouer, au
minimum, pour couvrir tous les cas et remporter les gains ? La réponse n'est
pas simple. Pour le cas (n, k, s), le problème revient à compter la quantité
minimale de k-gones pour couvrir tous s-tuplets sur un n-gone. Voir Exemple du
quadrilatère. |
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()