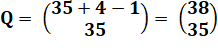|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Balles
réparties dans des boites Méthode "étoiles et
barres" ou "boules et bâtons" Quelles sont les façons de
disposer n balles dans k boites? Comment calculer la quantité
de possibilités? Même dans le cas où les
boites doivent contenir un minimum de balles.
La quantité (Q) de ces combinaisons avec répétitions (ou p-suites)
vaut: (la parenthèse symbolise le coefficient
binomial)
|
Anglais: Distributing balls into boxes or into bins
|
|
||
|
Aucun panier vide Repartir
4 œufs dans 3 paniers, aucun panier ne doit être vide. Simple!
On place d'abord un œuf dans chaque panier. L'œuf
restant est placé dans un des paniers, soit trois possibilités. |
|
|
|
Aucun panier avec moins de 2 œufs Répartir
9 œufs dans 3 paniers avec 2 œufs minimum par panier. Plaçons 2
œufs dans chacun des paniers. Il en reste 3 à distribuer dans trois paniers
qui peuvent être vides. |
|
|
|
Pour
résoudre le cas où un minimum d'œufs par panier est imposé, il
suffit de savoir traiter le cas de la distribution des œufs dans
des paniers qui peuvent être vides. |
||
|
|
|||
|
Répartir 4 œufs dans 3 paniers Cette
fois, on autorise les paniers vides. Premier cas: 4 œufs dans le panier A que nous
notons par le triplet (4, 0, 0); avec les 4 en B nous avons le triplet (0, 4,
0); etc. Deuxième cas: 3 œufs dans A et 1 en B avec la
notation (3, 1, 0) qui se décline trois fois en faisant jouer à B et C le
rôle de A. Etc. Il y a 15
façons de répartir 4 œufs dans trois paniers, certains paniers pouvant être
vides. |
Quinze possibilités
|
||
|
Configuration typique Le panier A est la référence. On cherche les possibilités avec 4, puis
3, puis 2 et enfin 1 œufs. |
Les trois configurations B et C joue aussi le même rôle que A. Notez que la somme des nombres d'un triplet vaut 4, la quantité d'œufs
à distribuer |
||
Partition
|
Le problème de répartition des
balles en boites est une manière de voir un problème plus général de la théorie des nombres: combien de
possibilités de partitionner
un nombre n en k termes? Les triplets ci-dessus donnent
toutes les possibilités de partitions du nombre 4 avec quatre termes. |
![]()
Comment calculer ?
Important:
nous sommes
dans le cas de balles identiques et de panier numérotés
Anglais: stars and bars method
|
Démonstration du théorème
"positifs" Cas où tous ont au
moins 1 objet dans la
distribution |
|
|
|
Étoiles en boites et en barres Imaginons
n objets à placer dans k boites. On
représente les n objets par des étoiles. Ces
étoiles sont à placer dans k boites, avec au
moins une étoile dans chaque boite. Les
boites sont numérotées de 1 à k, par contre les étoiles sont toutes
identiques. Seule la quantité d'étoiles dans kième boite nous intéresse. |
Exemple de k-uplet (ici: 7-uplet) Sept objets représentés par sept étoiles.
Boite n°1 Boite n°2 Boite n°3 Configuration représentée par le 3-uplet: (2, 3, 2). |
|
|
Méthode Les
étoiles étant placées en ligne, on en prend une quantité pour la boite 1,
puis une quantité pour la boite 2, etc. Les quantités
sont séparées par une barre (comme un trait de couteau ayant partagé la bande
d'étoiles). Aucune
boite vide: le trait se trouve donc entre deux étoiles et il n'y a jamais de
double trait. |
Les
barres de séparation montrent la répartition dans les boites. Il y a (k – 1)
barres pour k groupes d'étoiles. Et, avec n étoiles, il y a (n – 1) façons de
positionner une des barres. |
|
|
Formule Avec cette
manière de voir, le problème se résume à un choix de (k – 1) barres parmi (n
– 1) positions. Soit les combinaisons
de (k – 1) parmi (n – 1):
|
Il
s'agit de trouver tous les cas ou 2 barres sont placées parmi 6 possibilités. |
|
|
Démonstration théorème
"positifs ou nul" Cas où certains auront 0 objet dans la
distribution |
|
|
|
Dénombrement Ce cas
diffère du premier uniquement du fait qu'il permet les boites vides. Pour k
boites, il y a toujours (k – 1) barres de séparation, mais celles-ci peuvent être
doublées, signifiant que la boite entre les deux barres est vide. Nous
voici en présence de n étoiles et de (k – 1) barres, soit un total de (n + k
– 1) objets et pour matérialiser la position des barres, nous devons en
sélectionner (k – 1). |
Exemple de k-uplet Sept objets placés dans cinq boites. Configuration représentée par le 5-uplet: (0,
2, 0, 3, 2). Présence
de 7 étoiles. Et nous avons 4 barres pour 5 boites (k – 1), comme
précédemment; |
|
|
Formule Avec cette
manière de voir, le problème se résume aux possibilités de choisir (k – 1)
objets parmi (n + k – 1):
Ces sont
les coefficients
du binôme et, on sait qu'iles sont symétriques, d'où les deux égalités
(en remarquant bien que, en bas: (k – 1) ajouté à n donne bien le nombre du
haut). |
Exemple de calcul
Il s'agit
de trouver tous les cas ou 2 barres sont placées parmi 9 emplacements possibles. Choix
de 2 parmi 9 = 36 possibilités. Calcul:
avec n = 7 et k = 3
|
|
|
Il y a Q façons
de mettre n balles dans k boites, certaines pouvant être vides. |
Il y 36
façons de mettre 7 balles dans 3 paniers, certains paniers pouvant être
vides. |
|
|
|
||||||||||||||||||||
|
Dénombrement Cas où
l'on exige que chaque panier contienne au moins a balles. Alors on
place a balles dans chaque panier; ce qui fait un total de ak balles. Dès lors,
il faut distribuer les balles restantes (n – ak)
dans les k paniers, certains paniers pouvant être vides |
Formule générale
Possibilités
de distribuer n objets banalisés à
k personnes (donc non banales)
avec a objets au moins par
personne. |
|||||||||||||||||||
|
Pour au moins
une balle dans chaque panier, a = 1. On retrouve la formule indiquée. |
Cas ou a = 1 (au moins un objet par panier)
|
|||||||||||||||||||
|
Exemple 10 balles
(quelconques) dans 2 paniers avec 2 balles au moins dans chaque panier. Dans le
cas de balle numérotées, il ya 501 possibilités. |
Calcul
|
Répartition
|
||||||||||||||||||
![]()
|
|
||
|
On
dispose de 7 billets de 10 euros. Aubin,
Boris et Cyrille reçoivent chacun au moins un billet. Combien de possibilités
de distribution des 7 billets parmi ces trois personnes? |
n = 7 et k = 3 Les billets sont identiques, pas les
personnes. Application du théorème "positif"
|
|
|
10
bonbons à distribuer à 4 enfants. Combien
de possibilités sans restrictions? Et si
chaque enfant reçoit au moins un bonbon? |
n = 10 et k = 4 Les bonbons sont les mêmes par les enfants. Certains enfants peuvent ne pas avoir de
bonbons: applications du théorème "positif ou nul".
Dans le cas où chaque enfant reçoit au
moins un bonbon, application du théorème "positif".
|
|
|
Nous
commandons 12 glaces à la vanille, à la fraise et à la pistache. Combien
de possibilités de commandes? |
n =12 et k = 3 Il est en effet possible de ne pas prendre
un parfum: application du théorème "positif ou nul"
|
|
|
Nous commandons
9 glaces pour 9 enfants parmi 35 parfums. En
parfums, 3 enfants veulent toujours le chocolat, 2 veulent fraise et les
4 autres aiment la surprise. Combien
de possibilités de commandes? |
Une fois les commandes faites pour les 5
qui savent ce qu'ils veulent, il reste 4 glaces à commander parmi 35 parfums.
Chocolat et fraise sont toujours en lice. n = 35 et k = 4
|
|
|
À
partager entre quatre personnes, on dispose de:
Chacun
doit recevoir 2 pâtisseries de chaque sorte. Notez que: cela revient à distribuer séparément chacune des
pâtisseries. Celles-ci sont banalisées mais pas les personnes: application du
théorème "positif" avec a minimum. |
Trois distributions
indépendantes, alors, les possibilités sont multipliées Q = 35 x 10 x 1 = 350 |
|
Avec des nombres –
Quantité de partitions
|
Pour des
nombres entiers positifs ou nuls, on a l'équation: a + b + c + d =
11 Combien
de solutions possibles? |
n = 11 et
k = 4
|
|
On a
l'équation: a + b + c + d =
13 avec a
> 2, b > -3, c > -1 et d > 0 Combien
de solutions possibles? |
On se ramène au cas précédent en faisant un
changement de variables a' = a – 3 b' = b + 2 c' = c d' = d – 1 a' + b' + c' + d' = a – 3 + b + 2 + c + d –
1 = a + b + c + d – 2 = 1 3 – 2 = 11 a', b', c' et d' sont positifs ou nuls. Q = 364 (exemple précédent) |
|
Pour des
nombres entiers positifs ou nuls, on a l'équation: a + b + c = 0 Avec a, b
et c Combien
de solutions possibles? |
Changement de variables a' = a + 5, b' = b + 5 et c' = c + 5 a' + b' + c' = a + 5 + b + 5 + c + 5 =
a + b + c + 15 = 0 + 15 = 15 a', b' et c' sont positifs ou nuls.
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/Denombre/aaaBalle/Balle01.htm
|
![]()