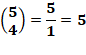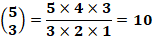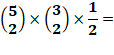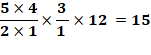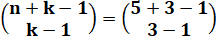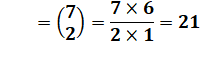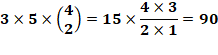|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Balles réparties en boites (ou paniers) sous conditions Nous
disposons de n balles à répartir dans k paniers (boites, sacs, ou urnes). Quelle
est la quantité de possibilités; quelle est la quantité de configurations
possibles? Note: nous utiliserons le panier. Ainsi, la lettre B symbolise la Balle et
la lettre P, le Panier. Calcul des possibilités selon les
conditions Paniers
et balles peuvent être banalisés ou individualisés. Les paniers peuvent se
retrouver vides ou alors comporter au moins une balle.
Voir aussi Balles numérotées dans k boites sous contrainte |
|||||||||||||||||
Anglais: Multiset, bag / Distributing balls into boxes
|
|
||
|
Exemple: 3 balles dans 2 paniers Imaginons;
Comment
je m'y prends? Attention, un panier peut être vide. Je prends la balle B1 que je mets dans un des
deux paniers: 2 possibilités. Je prends la balle B2 que je mets dans un des
deux paniers: 2 possibilités. Je prends la balle B3 que je mets dans un des
deux paniers: 2 possibilités. Ce sont
trois événements indépendants, le total des possibilités est le produit
des possibilités de chacun: Q = 2 x 2 x 2 = 23 Note: les balles sont numérotées ou de couleurs
différentes ou repérées d'une manière
quelconque. Chacune est bien identifiée. Même
remarque pour les paniers, pourvu qu'ils soient bien identifiés; ils sont non
interchangeables, non banalisés. |
Illustration
3 balles dans deux paniers: 23 = 8 façons de faire. Tableau Il montre ces 8 répartitions:
|
|
|
Une autre manière de compter les
configurations (sans en oublier)
Lecture des chiffres à droite: 123
000 veut dire que les balles 1, 2 et 3
sont dans le panier 1 et aucune dans le panier 2. |
||
|
D'une
manière générale, avec
C'est le
même type de dénombrement que sur un
compteur. C'est une p-liste. |
Q = kn répartitions possibles |
|
Voir Sélection
ou distribution
|
|
||
|
5 balles numérotées dans 3 paniers
numérotés En accord avec ce que nous venons de voir: |
Q = 35 = 243 |
|
|
5 balles quelconques dans 3 paniers
quelconques Il y a
seulement cinq possibilités, et on les énumère: Remarquez, par exemple, que les cinq balles soient dans le panier 1 ou 2 ou 3,
peu importe; on ne compte qu'une seule possibilité. |
{5, 0, 0} {4, 1, 0} {3, 2, 0} {3, 1, 1} {2, 2, 1} |
|
Anglais: How many ways
are there to distribute 5 balls into 3 boxes, according to conditions?
|
|
||
|
Pour les
cas vus précédemment, voyons ce chacun devient lorsque les balles sont
numérotées. Numérotées
ou pas, il y a un seul cas avec 5 balles dans un panier (les 3 paniers ne
sont pas repérés). Pour 4 balles
dans un panier parmi 5, il y a 5 possibilités: Pour 3
balles dans un panier parmi 5, il y a 10 possibilités; on met les deux autres
dans l'un ou l'autre panier, c'est sans importance: C'est la
même chose pour le cas suivant; on met une balle dans l'un des paniers et une
balle dans l'autre. Enfin,
pour le dernier cas, on choisit 2 balles parmi 5, puis 2 balles parmi 3.
Cependant, les 2 parmi 3 peuvent être placées indifféremment dans un des 2
paniers qui restent; il faut diviser par 2 Méthode alternative Parmi les
243 fossilités avec numérotation, voyons celles qui se réduisent du fait de
la numérotation des balles. Le cas
{5, 0, 0} permet 3 possibilités qui, avec la numérotation des balles, devient
une seule. Reste 240
cas à analyser. Pour chacun, il existe 3! = 6 possibilités de permutations,
soit 204 / 6 = 40 possibilités du fait de la numérotation des balles. |
{5, 0, 0} =>
1 cas {4, 1, 0} =>
5 cas
{3, 2, 0} => 10 cas
{3, 1, 1} => 10 cas
{2, 2, 1} => 15 cas
Total: 1 + 5 +
10 + 10 + 15 = 41 Décompte
alternatif 243 = 240
+ 3 3 => 1 240 => 240/3! = 40 24
=> 1 + 40 = 41 |
|
|
|
||
|
Le
décompte classique peut être repris. Avec {5,
0, 0} et trois paniers différents, il y a 3 possibilités de mettre 5 balles
dans un panier. Avec {4,
1, 0} et {3, 2, 0}, les trois comptes étant différents, les 3! = 6
permutations sont toutes possibles. Avec {3,
1, 1} et {2, 2, 1}, parmi les 6 permutations possibles, seules la moitié est
à retenir car dans les deux cas, deux paniers jouent le même rôle. Méthode alternative La
méthode des étoiles et des barres donne
directement le décompte. En
l'occurrence les balles comptent pour n = 5 et les k = 3 paniers pour 2
barres. Notre
problème se résume au choix de l'emplacement de 2 barres parmi 7 emplacements. |
{5, 0, 0} => 3 cas {4, 1, 0} => 6 cas {3, 2, 0} => 6 cas {3, 1, 1} => 3 cas {2, 2, 1} => 3 cas Décompte alternatif
|
|
|
5 balles numérotées dans 3 paniers numérotés,
sans paniers vides |
|
|
|
Du cas
classique, nous retirons les cas avec paniers vides. Restent les cas {3,1, 1}
et {2, 2, 1}. Cas avec
3 balles dans un des paniers:
Cas avec
1 balle dans un des paniers:
Voir Formule
de calcul
|
{5, 0, 0} => non {4, 1, 0} => non {3, 2, 0} => non {3, 1, 1} => 60 cas
{2, 2, 1} => 90 cas Total 60 + 90 = 150 cas |
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/Denombre/aaaBalle/Multiset.htm
|
![]()