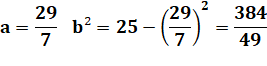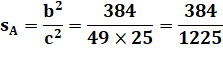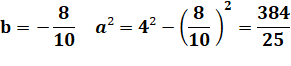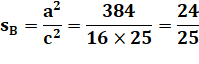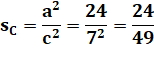|
Édition du: 13/01/2025 |
|
INDEX |
Théorème de Pythagore – Extensions |
|||
|
Pythagore en linéaire (triple quad) |
||||
![]()
|
Trigonométrie rationnelle Trigonométrie de Wildberger
Une forme
particulière de la trigonométrie,
de la science des mesures notamment dans le triangle.
Elle a la particularité de ne pas utiliser de nombres
irrationnels: ni nombre Pi, ni
racines
carrées. Toutes les grandeurs sont exprimées par des fractions.
Son auteur, N.J. Wildberger; affirme
que cette trigonométrie est plus pratique et permet de résoudre plus
simplement certains problèmes de géométrie. |
||
|
|
Sommaire de cette page >>> Trigonométrie rationnelle – Notions >>> Calcul de l'ouverture >>> Triangle rationnel complet >>> Bases de la trigonométrie rationnelle >>> Les cinq lois fondamentales |
Débutants Glossaire |
Anglais: Triple quad formula
Le niveau du
lycée suffit pour aborder cette page.
|
Traditionnelle Les côtés du triangle sont définis par leur longueur. Les angles par leur valeur en radians ou en degrés; généralement des
nombres avec décimales, ici tronquées à deux. |
Rationnelle Les côtés du triangle sont définis par le carré de leur longueur: la quadrance. Les angles par une fraction qui équivaut au carré du sinus de l'angle:
l'ouverture (spread en anglais) |
|
|
|
|
|
Voir Brève
789
|
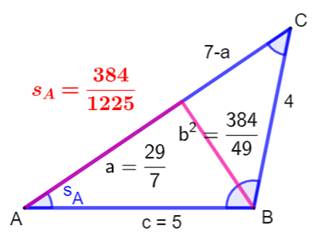
Exemple pour l'angle en A On trace la hauteur en B dont la longueur est b. Le pied définit le
segment de longueur a et celui de longueur (7 – a), pour notre exemple. Théorème
de Pythagore: Différence: On connait a puis b: Calcul de l'ouverture (carré du sinus):
|
Triangle avec ouverture en A
sA est l'ouverture (spread) de l'angle en A. C'est la valeur du sinus de l'angle au carré. Toujours une valeur rationnelle. |
||
|
Pour l'angle en B
|
|
||
|
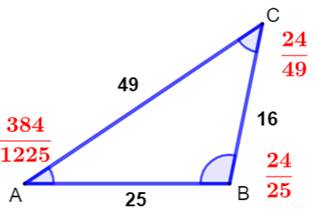
Pour l'angle en C
|
|
||
|
Commentaire |
On pourrait limiter l'explication à deux figures.
En effet, la première figure pourrait donner
l'ouverture de l'angle en C avec sC = b² / 4² = 24/49 De même, la second figure pour l'angle en A avec
sA = a² / 49 = 384/1225 Également pour la troisième figure qui donne sB
avec sB = a²/25 = 24/25 En choisir deux parmi trois suffirait, même si on
comprend l'idée de donner les trois. |
||
Voir Calcul
d'une hauteur rationnelle
|
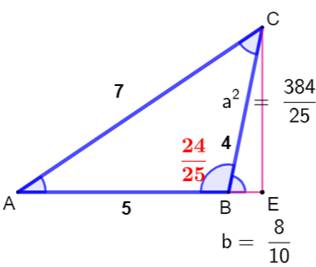
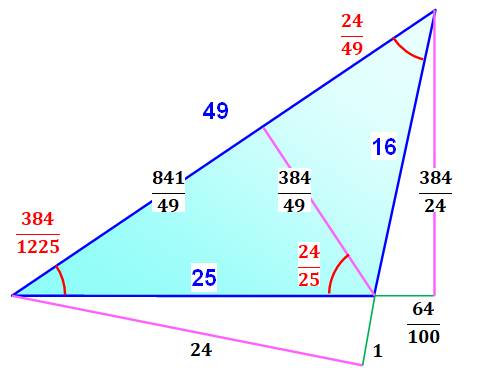
Triangle (4, 5, 7) On récapitule les mesures du triangle rationnel. Toutes les grandeurs sont rationnelles (des fractions) et non des
nombres avec radicaux. Attention, toutes ces valeurs sont des carrés. Par exemple le côté marqué 49, mesure en fait 7. Les angles sont exprimés par le sin² des angles. |
|
|
|
Bilan Outre son emploi en trigonométrie rationnelle, voyez comme cette
méthode permet de trouver les fractions exactes
qui représentent les angles et les longueurs des côtés et des hauteurs. |
||
|
Quadrance Soit deux points de coordonnées: |
Q(A1, A2) = (x2 – x1)² + (y2
– y1)² |
|||
|
Quadrance Une droite L d'équation ax + by + c = 0 est notée (a, b, c) Avec deux droites L1 et L2, l'ouverture est définie par cette
relation: |
|
|||
|
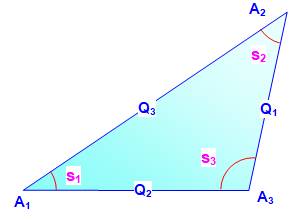
Pour trois points (un triangle)
|
|
|||
|
Théorème de Pythagore |
Les
droites A1A3 et
A2A3 sont perpendiculaires
|
|
|
Formule du triple quad |
|
|
|
Loi des ouvertures |
Triangle dont
aucune quadrance n'est nulle
|
|
|
Loi des croisements |
|
|
|
Formule de la triple ouverture |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Voir liste des
liens pour le théorème de Pythagore |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Pythagore/TrigoRat.htm
|