NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/01/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Puissances
Débutants Logarithmes	Théorème de Pythagore			Glossaire Puissances
Rubrique PARTITION INDEX PUISSANCES	Th de Pythagore		Triplets
	Démonstration du théorème		Exemples de calculs
		Sommaire de cette page >>> L'arbre coupé >>> La lance de Fibonacci >>>Problème de Brahmagupta >>> Avec l'aire >>> Avec le périmètre >>> Les deux tours

THÉORÈME DE PYTHAGORE

Exemples de calculs

Quelques exemples typiques de calcul.

L'arbre coupé
Un arbre se casse en deux, tout en restant attaché au tronc Il a une taille h de 10 mètres et coupe à la hauteur de 4 mètres. Quelle est son emprise au sol d. Le théorème de Pythagore: d² = e² – h² = (H – h)² – h² = H² – 2Hh Soit la longueur du segment d: d² = 100 – 80 = 20 d = 4,47… m Ou calcul numérique direct d² = 6² - 4² = 20 = 4,47213…²

La lance de Fibonacci
Vers 1200, Léonard de Pise dit Fibonacci pose le problème suivant: Une lance de 20 pieds est posée verticalement le long d'un mur. Si on écarte le bout au sol de 12 pieds de combien descend le bout le long du mur? Le théorème de Pythagore: BC² = BD² – CD² = 20² – 12² = 400 – 144 = 256 = 16² Soit la longueur du segment AB h = AB = AC – BC = 20 – 16 = 4 Le pied vaut environ 30 cm.

Problème de Brahmagupta
Vers 600, Brahmagupta, mathématicien indien, pose le problème suivant: Deux sorcières* en haut d'un mur décident de rejoindre le village. L'une prend le chemin normal. L'autre choisit la magie: elle prend de la hauteur et se laisse voler en ligne droite vers le village. Quelle est la hauteur d'envol pour égaliser les trajets? * l'original parle d'ascètes. Égalité des trajets: En développant:
Exemple numérique: h = 100, d = 800 => Plus petite solution entière: h = 2, d = 4 => La suivante: h = 3, d = 3 =>		e = 80 e = 1 e = 1

Avec l'aire
Dans ce triangle rectangle, l'aire est connue de même que l'un des côtés. Trouvez la mesure des deux autres côtés.
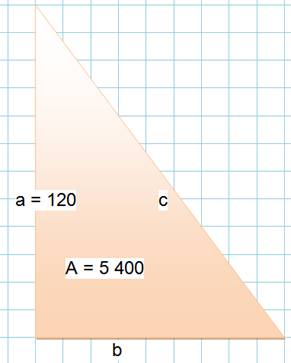
Théorème de Pythagore	a² + b² = c²	120² + b² = c²
Aire du triangle	A = 1/2 a . b b = 2A / a	5 400 = 1/2 x 120b b = 10 800 / 120 = 90
Calcul de c	c² = a² + (2A/a)²	c² = 120² + 90² = 14 400 + 8 100 = 22 500 c = 150

Avec le périmètre
Dans ce triangle rectangle, le périmètre est connu de même que l'un des côtés. Trouvez la mesure des deux autres côtés.
Théorème de Pythagore	a² + b² = c²		100² + b² = c²
Périmètre du triangle	P = a + b + c b = P – a – c		300 = 100 + b + c b = 200 – c
Substitution de b	a² + ((P – a) – c)² = c²		100² + (200 – c)² = c²
Développement	a² + (P – a)² – 2(P – a)c + c² = c²		100² + 200² – 400c + c² = c²
Soustraction de c²	a² + (P – a)² – 2(P – a)c = 0		50 000 – 400c = 0
Calcul de c			c = 50 000 / 400 = 125
Calcul de b	b = P – a – c		b = 300 – 100 – 125 = 75

Exercice

Faire le calcul avec a = 52 et P = 156

Solution: c = 65 et b = 39

En effet: 52² + 39² = 2 704 + 1 521 = 4 225 = 65²

Et P = 52 + 39 + 65 = 156

Les deux tours
Sur la figure, calculez la valeur de x pour que, A, B et l étant donné, les deux obliques soient de même longueur (H). Ce problème est souvent présenté comme le problème de deux oiseaux s'envolant chacun d'une tour et piquant vers le sol à la même vitesse. Quelle est la position du point au sol visé par es oiseaux?
Calcul littéral, avec le théorème de Pythagore s'appliquant dans les deux triangles rectangles.
En fixant A = 100 et L = 100, comment varie x en fonction de B? x = B² / 2L = B² / 200 Exemples: B = 60, alors x = 18 et pour B = 100, alors x = 50

SUITE	Démonstration chinoise … Toutes les relations dans le triangle quelconque
Voir	Addition - Glossaire Années Pythagore Approximation de Pi avec les triplets Décade de Pythagore Énigmes – Index Pythagore - Biographie Toutes les relations dans le triangle quelconque
Aussi	Bi, tripartitions Bouleversements et crises en maths Cercle Conjecture de Riemann Conjecture d'Euler Nombre = sommes de puissances Nombres carrés Nombres polygones Nombres triangles Partitions Petit théorème de Fermat Somme multi puissantes Théorie des nombres Triangle Unité des puissances
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/ThPythCa.htm