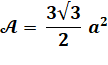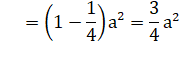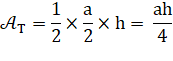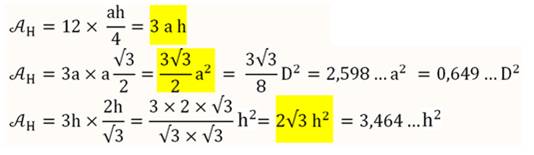Hexagone

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/08/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Polygones
Débutants Général	HEXAGONE					Glossaire Général
INDEX Polygones Géométrie	Généralités	Dimensions		Pavage	Rosace
	Hexagramme	Construction		Puzzle	Magique
	Nombres hexagonaux		Triangle dans l'hexagone		Ramsey
		Sommaire de cette page >>> Hexagone >>> Tracé de l'hexagone au compas >>> Calcul de l'aire de l'hexagone régulier >>> Construction >>> Hexagone de Graham >>> Étoile mystique de Pascal >>> Théorème de Pappus >>> Quelques hexagones typiques

HEXAGONE & ÉTOILE à 6 branches

La FRANCE est en forme d'hexagone, avec six côtés réguliers:

Trois côtés sont maritimes, et

Trois côtés sont terrestres.

Pavage avec des hexagones

HEXA GONE

du grec:

hexa, six,

gônia, angle

Les SIX-GONES sont de retour! ou

Gambas les SIX-GONES

Quand passent les cigognes:

film soviétique de Mikhail Kalatozov – 1957.

Gone est synonyme de gosse, moufflet …

Voir Pensées & humour / Épigone

Les flocons de neige (snowflake) ont la forme d'étoiles à 6 branches.

Les alvéoles des ruches sont hexagonales

(The cells of a beehive honeycomb are hexagonal)

Devinette

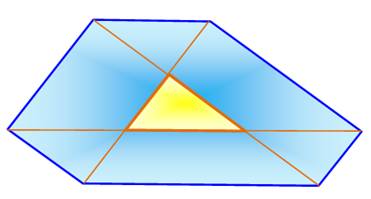
Cet hexagone irrégulier est construit à partir d'un triangle quelconque.

Chaque côté est prolongé de part et d'autre d'une longueur précisément égale à celle du côté prolongé.

Quelle est l'aire de l'hexagone en fonction de cette du triangle ?

Brève 363

Solution

HEXAGONE

Polygone Hexagone régulier Angles intérieurs Périmètre	à six côtés les six côtés sont égaux (a) 120° 6a
Aire hexagone régulier
Aire hexagone régulier unité Aire du cercle de même rayon unité	2, 598076 … 3, 1416 …
Pavage	infini du plan (comme triangle équilatéral ou le carré).

Anglais: hexagon (sexagon). An hexagon is a six-sided polygon

Tracé de l'hexagone régulier au compas

· Dessin initial du cercle rose.

· Avec la même ouverture du compas, choisir un point quelconque sur ce cercle et dessiner le cercle bleu.

· En conservant l'ouverture du compas, dessiner le cercle vert ayant pour centre un des points d'intersection des deux premiers cercles.

· Le segment rouge est l'un des côtés de l'hexagone.

· Poursuivre la même procédure pour les autres côtés.

Notez que cette construction permet la trisection de l'angle de 180° en angles de 60°.

Tracé complet

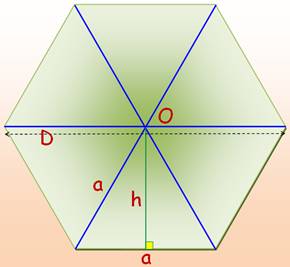
Calcul de l'aire de l'hexagone régulier
· L'hexagone régulier est formé de six triangles équilatéraux de côté a ou de 12 triangles rectangles de côtés: a, a/2 et h. · Avec Pythagore: · Aire du triangle rectangle: · Aire de l'hexagone:	h est l'apothème

Voir Construction / Autres mesures dans l'hexagone / Six cercles +1 / Rosace

Merci à Patrick H.

HEXAGONE DE GRAHAM (1975)
· Aire de l'hexagone régulier de diamètre unité. · Aire de l'hexagone de Graham: diamètre unité et aire maximale. · Supplément de surface entre les deux		0, 649 519 … 0, 674 981… 3,92 %
· Alors que l'aire de l'hexagone régulier est connue directement
· Celle de l'hexagone de Graham est racine de l'équation	4096 x¹⁰ +8192x⁹ − 3008x⁸ − 30848x⁷ + 21056x⁶ + 146496x⁵ − 221360x⁴ + 1232x³ + 144464x² − 78488x + 11993 = 0

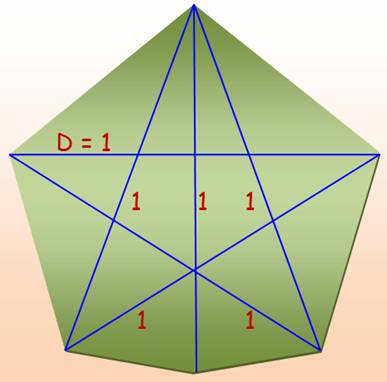
Anglais: Graham's biggest little hexagon.

Polygon whose diameter is 1, and it has largest area.

ÉTOILE MYSTIQUE de Pascal

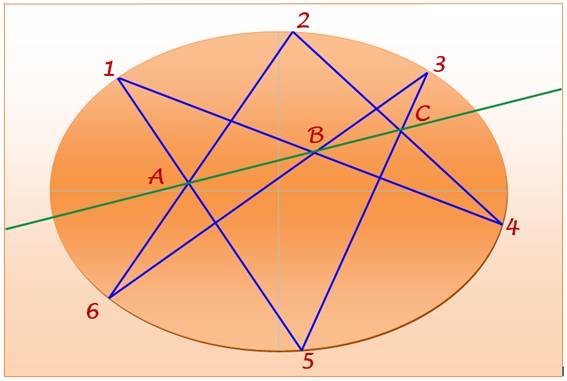
Hexagramma Mysticum

· Découverte par Pascal en 1640, à l'âge de 16 ans.

· Six points sur une conique (1, 2, 3, 4, 5, 6).

Les intersections A, B, C sont trois points alignés.

· Les six points forment un hexagone. Soit le théorème:

Dans tout hexagone inscrit dans une conique, il existe trois couples de cordes dont les trois points de concours sont alignés.

Voir Théorème de Pascal / Théorème de Brianchon

Théorème de Pappus

· Un cas particulier avait déjà été trouvé par Pappus d'Alexandrie (vers 300 ap. J.-C.)

· Deux droites, trois points quelconques sur chacune des deux droites.

Les droites dessinées, celles qui joignent les deux points autres que le vis-à-vis, se coupent en trois points alignés. Les pointa A, B et C sont situés sur la droite de Pappus.

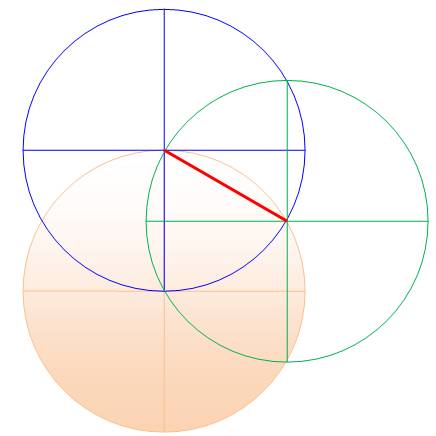
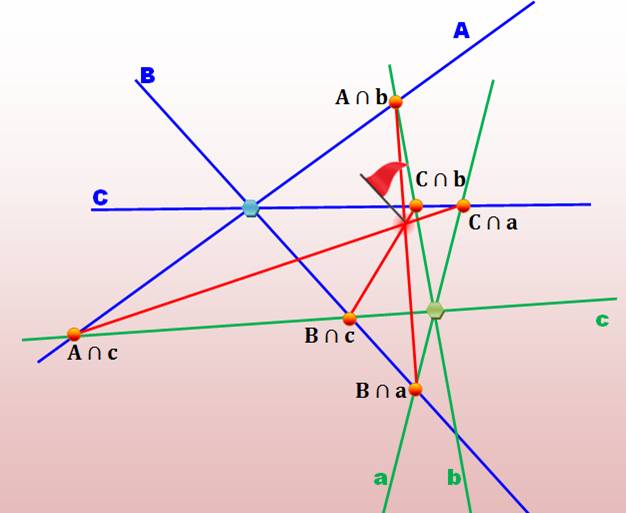
Réciproque du théorème de Pappus

· Soit deux points, et trois droites passant par chaque point.
On obtient six points d'intersection. Les trois droites les reliant deux à deux sont concourantes.

· Plus précisément:

· Les trois droites bleues concourantes (A,B,C) et les trois vertes (a,b,c);

· Les couples de points d'intersection: (A,c) et (C,a) ; (A,b) et (B,a); et (B,c) et (C,b) sont reliés pour former les trois droites rouges.

· Ces trois droites rouges sont concourantes, dit la réciproque du théorème de Pappus.

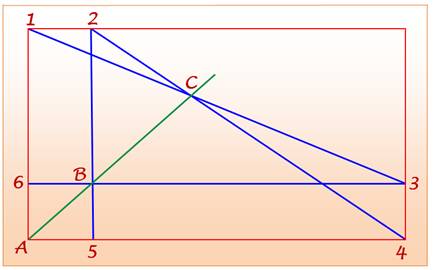
Cas du rectangle (droites parallèles)

· Un cas particulier est constitué par le rectangle. Il existe 6 combinaisons de ce type dans un rectangle:

Voir Théorème de Ménélaüs / Homologie / Points / 10 Arbres / Théorème de Pappus-Clairaut

Devinette – Solution

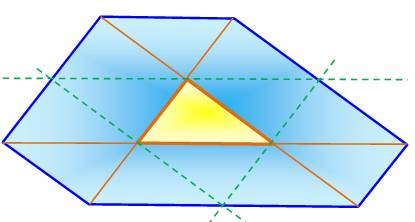
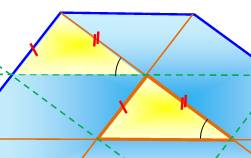
Le tracé des parallèles (en vert) à chaque côté du triangle et passant par le sommet opposé, révèle une figure comportant 12 triangles qui sont égaux* au triangle original.

L'aire de l'hexagone est donc égale à 13 fois celle du triangle originel.

H = 13 t

Explications

Les triangles formés par le prolongement des côtés sont égaux: un angle égal et deux côtés égaux (Illustration du milieu).

Du fait du tracé des parallèles, les autres triangles (Illustration du bas) sont également égaux: un angle égal et deux côtés égaux.

* Aujourd'hui, on dit superposables ou isométriques.