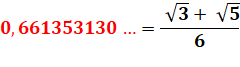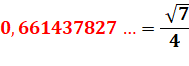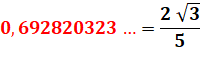|
|||||||||||||||||||||||||
![]()

|
0,65 = 65 / 100
= 13 / 20 = 2/3 – 1/60 |
|
|
|
|
|
0, 652173913… = 15/23 0,6521739130434782608695
652… |
|
|
|
|
|
|
![]()
|
|
|
|
|
|
|
0,6601618 …
|
|
|
|
|
0,666 … = 2/3 |
Voir Autres
propriétés en 1/3 |
|
|
|
|
1
– (5/6)4 = 0,518 |
|
Voir Nombre 666 –
Nombre de la Bête
|
Art |
|
|
|
|
|
0,670 873 479…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, 68…
|
0,68 = 17/25 = 68/100 |
|
|
|
|
|
0,681818… = 15/22 |
|
|
|
|
|
|
|
|
0, 684210526…
=
13/19 0,684210526315789473
684… |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6922006276 0,3678794412 |
|
|
|
0, 692307692…
=
9/13 0,692307 692307… |
||
|
|
|
|
|
0,693 147 … = ln 2 =
loge 2 = 1 – 1/2 + 1/3 –
1/4 + 1/5 - 1/6 + … = 1/2 + 1/12 +
1/30 + 1/56 + … |
Note log 10 2 = 0,301 029 99 ... Suite en
Logarithme
- valeur |
|
|
|
||
|
|
||
|
|
||
![]()
![]()