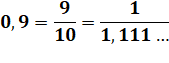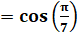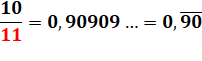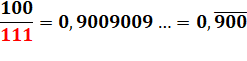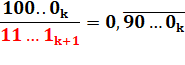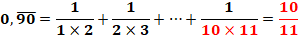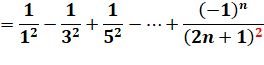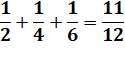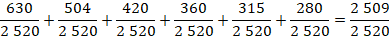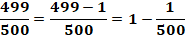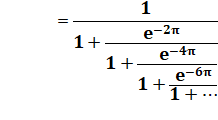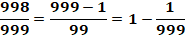nombre de 0,9 à 1

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/01/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres	DicoNombre NOMBRES			Glossaire Nombres
0,7 / 0,8 0,6 / 0,5 / 0,4 0,1 0,01 0,001 0	0,9 à 0,99			1 2 5 10 100
Sommaire =>	Maths 0,9…	0,95…	0,99…
	Culture 0,9…		0,99…

Nom des nombres / Fractions

Égalité surprenante!

0, 9

Le nombre décimal 0,09 (0,09000…) est le développement décimal de la fraction 1/ 11,111… nombre périodique infini.

0,9 = 9/10 = 1/2 + 1/3 + 1/15		Fractions égyptiennes
0,900 968 868…		La trigonométrie de Pi/7 est particulière. Angle intervenant dans l'heptagone.
			Densité minimale de la disposition des octogones réguliers pour paver le plan.
				Fonction GAMMA 1/4.
0, 906 899 682 …	Aire occupée dans un plan par des cercles identiques placés en réseau hexagonal, de sorte que chacun en touche 6 autres. Densité maximale d'un empilement de disques dans un plan; il s'agit d'une disposition en triangle. Avec une disposition en carré, la densité devient: 78,53% =

	Nombres périodiques avec motif qui se répète.
0, 90 90 … = 10 / 11 0, 9900 9900 … = 100 / 101 0, 999000 999000 … = 1000 / 1001 Etc.	Nombres périodiques. Noté avec un surlignement sur les chiffres de la période:
		La somme de tous les inverses de produits de deux consécutifs jusqu'à n est égal à n / (n+1). Voir Brève 513 pour exemple de calcu et Brève 524.

0, 915 965 594 177 219 015 05 …

Constante de Catalan, sans doute transcendante, mais non prouvé.

On ne sait pas si la constante de Catalan est rationnelle ou irrationnelles.

Bêta (2) est la fonction bêta de Dirichlet, avec l'inverse des nombres impairs mis à la puissance 2.

Exemple de calcul avec Maple

0,91666… = 11 / 12

Objet d'une célèbre énigme de partage:

Un père met 11 bonbons sur la table et dis à son ainé dans prendre la moitié, son deuxième le quart et le dernier un sixième. Comment faire le partage?

L'un d'eux à une idée: il demande à son père de lui prêter un bonbon supplémentaire.

Chacun se sert: 6 pour l'ainé, 3 pour le cadet et 2 pour le dernier. Total 6 + 3 + 2 = 11 bonbons.

Il en reste un qui est rendu au père.

Voir Partage des 17 chevaux

		Identité de Bill Gosper.
	Densité maximale (conjecture) des triangles de Reuleaux.
	Angle de l'octogone.
0,93333… = 14 / 15
	Exponentielle d'exponentielle …
0,939692…	Demi-angle au centre de l'ennéagone. Voir Calcul.
0,94444… = 17 / 18	Objet d'une célèbre énigme de partage. Voir Partage des 17 chevaux

0, 95

0,95 = 19 / 20
0,951 0 … 0,95105651629515357211…	Imaginaire dans la racine 5^e de 1.
0,96 = 24 / 25
0, 96592 58262 89068 28675 …	Valeur de cosinus Pi sur 12 Angle qui vaut 15°. Côté du carré inscrivant un triangle équilatéral de côté unité.
0,96666… = 29 / 30
0,972222… = 35 / 36
0,975 = 39 / 40
0,97777… = 44 / 45
0,98 = 49 / 50
0,98181818… = 54 / 55
0,983333… = 59 / 60
0,986666… = 74 / 75
0,9875 = 79 / 80
0, 98765 4320 987 … = 80 / 81	Nombre périodique remarquable avec les chiffres décroissants de 9 à 2
0,98333… = 89 / 90
0,98 98 98… = 98 / 99 0,988 988 … = 988 / 999 0,9888 9888 … = 9888 / 9999 Etc.	Nombres périodiques. Explication

0, 99

0,9900 9900 99… = 100 / 101 0,99 09 09 09… = 109 / 110 0,99 099 099… = 110 / 111
0,993333… = 149 / 150
0,99417 71762 … = 1/ log ₂ 10 + 1 / log ₂ e	Expression d'un logarithme en base 2.
0,995 = 199 / 200
0,995634920634921… = 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + 1/9	Somme d'inverses successifs. Pratiquement égale à 1. Mais il y a mieux en quatre fractions.
Somme des fractions mises au même dénominateur:
0,996 = 249 / 250
0,9975 = 399 / 400
0,998 = 499 / 500	Explication (principe valable pour tous les nombres de ce type:

Fraction continue de Ramanujan impliquant le nombre d'or

0, 99 888 45091… = sin(Phi)	Sinus du nombre d'or
0,998 998 … = 998 / 999 0,9988 9988 … = 9988 / 9999 0,99888 99888 … = 99888 / 99999	Nombres périodiques. Explication
0,9990000 999000 … = 1000 / 1001 0,9990 9990 … = 1110/ 1111
0,9991111… = 1124 / 1125
0,9992 = 1249 / 2000
0,9995 = 1999 / 1250
0,99999020… = sin (11) 0,99₁₆ 7857… = sin (2017 )	du fait que 7Pi/2 = 10,9955 … Trouvé par Trott en 2004 (ref. Mathworld)
0,999 999 …_{infinité de 9} = 1 = 0, 9 + 0, 09 + 0, 009 + ... = 1	Nombre périodique repdigit. Égalité surprenante. Voir Nombre 9,999… / Explications

Culture 0,9

Il faut 10 pour cent des efforts pour faire les 90 premiers pour cent du travail.

Il faut 90 pour cent des efforts pour faire les 10 derniers pour cent du travail.

Arthur Bloch, Murphy's Law, 1977

Voir Pensées & humour / Loi de Pareto

Cosmologie	90% de la masse de l'Univers est de la matière noire, non directement observable.		>>>
Biologie	90% des plantes vivent en symbiose avec des champignons. Les racines colonisées forment un organe mixte que l'on nomme mycorhize (myco: champignon et rhize: racine).		>>>
Nucléaire	>90% d'enrichissement de l'uranium nécessaire pour bien faire fonctionner une bombe nucléaire (70% le minimum).		>>>
Unité	0,9144 mètres = 1 yard = 3 pieds = 36 pouces	Unité légale en Grande-Bretagne (yd) du système "imperial metric" Inventée pour mesurer le tissu: longueur du menton au bout des doigts. Au XII^e, vaut la distance entre le nez du roi Henri I^er d'Angleterre et le bout de son médium.

Biologie

0,947 Indice moyen de Manning pour les hommes.

>>>

Quatre-vingt-quinze fois sur cent

La femme s'emmerde en baisant

Qu'elle le taise ou qu'elle le confesse …

Georges Brassens

Voir Pensées & humour

Probabilités	95% de probabilité d'avoir deux anniversaires identiques dans un groupe de 46 personnes.	>>>
Social	95% de la population humaine était occupée aux travaux agricoles en 1900.	>>>
Énergie	96% de l’énergie en Europe 2002 est d’origine fossile, nucléaire et hydraulique.	>>>
Économie	97% des unités d'habitation en France en 2010 possèdent au moins une voiture. 58% en ont deux.	>>>

Culture 0,99

Biologie	99% des molécules d'un être humain se détruisent en l'espace d'une année.
Probabilités	99% Probabilité que deux personnes ayant chacun une relation en France, ces deux personnes se connaissent	>>>
Relativité	99% de la vitesse de la lumière. Il faudrait voyager à une vitesse très proche de celle de la lumière pour vraiment profiter de la dilatation du temps.	>>>
Musique	0, 997 914 046 = 2⁸⁴ / 3⁵³ = 2ⁿ / 3^m Ratio utilisé en musique. Il permet de diviser l'octave (1/2) en quintes (1/3) successives jusqu'à se rapprocher le plus possible de 1.	>>>
Astronomie	99,85 % masse du Soleil dans le système solaire. Planètes: 0,14 %, satellites des planètes + astéroïdes, comètes: 0,01 %	>>>
Linguistique	J'en suis à 99 % sûr => Pratiquement certain.	>>>
Physique	99,999999999999 % Vide dans l'atome. Le noyau dans l'atome: une orange au centre d'une très grande place circulaire.	>>>

Retour

Suite

Nombres en 0,8

Nombre 1

Voir

Nom des nombres

Cette page

http://villemin.gerard.free.fr/NombDico/PetitNB/Pt09.htm

Liens sur ces pages >>>