|
||||||||||||||||||||||||||||||||
![]()
|
INTERVALLE ENTRE PREMIERS Écarts entre nombres premiers
Combien
sont-elles à posséder ce même écart ?
|
Voir Observations
sur les écarts entre nombres premiers
Anglais: Prime gap / difference between two successive prime
numbers.
|
L'écart entre les
nombres premiers 317 et 331 est de 14.
Il n'y a pas d'autres nombres premiers entre les deux. On considère
parfois l'intervalle (gap) qui compte les
nombres entre deux premiers (13, pour l'exemple cité). Le théorème
des nombres premiers indique que l'écart moyen entre deux premiers
consécutifs jusqu'à n est égal à ln (n). Le mérite d'un écart
entre premiers est le rapport entre cet écart et l'écart moyen à ce niveau de
nombres. Pour le couple (314, 331) on a m = 14 / ln(314) = 2,43… Zhang a prouvé qu'il y une infinité d'écart plus petits
que 70 000 000. Sachant que l'écart peut être aussi grand qu'on le souhaite!
En effet: n! +m est divisible par m pour m C'est une autre chose que de les connaitre. La course
au plus grand écart est intense, et en 2017, le mérite connu dépasse 40. Record 2017:
|
|
Nombres premiers Écart entre consécutifs Intervalle (gap) entre consécutifs (= écart – 1) [0, 1, 1, 3, 1, 3, 1, 3, 5, 1, 5, 3, 1, 3, 5, 5, 1, 5, 3, 1, 5, 3, 5, 7, 3] Somme des intervalles (cumul sur liste
précédente) [0, 1, 2, 5, 6, 9, 10, 13, 18, 19, 24, 27, 28, 31, 36, 41, 42, 47, 50, 51, 56, 59, 64, 71, 74] Somme des intervalles divisibles par 100: [plus grand premier, somme] [613, 500],
[2693, 2300], [3833, 3300], [4513, 3900], [6659, 5800], [7561, 6600], [8009,
7000], [8123, 7100], [9133, 8000], [9811, 8600], … |
![]()
|
|
|
|
·
Écart record entre deux nombres premiers successifs:
Tous les
nombres premiers jusqu'à 100 sont distants de moins de 7, sauf 89 et 97. Voir
Barre magique ·
Jusqu'à 97, on trouve les nombres pairs successifs,
mais la séquence est vite interrompue. ·
Voici les deux écarts qui manquent entre 8 et 14 149 – 139 = 10 211 – 199 = 12 |
|
|
|
|||
|
Distribution ·
Parmi les petits nombres, il y a beaucoup de nombres
premiers. Mais, parmi les grands nombres, ils sont de plus en plus rares. ·
L'écart moyen entre deux nombres premiers répond à un modèle simple:
·
Ce n'est qu'une moyenne, il y a beaucoup de dispersion Écart minimum ·
Les nombres premiers jumeaux ne
sont distants que de 2. Réduire l'écart ·
Une recherche consiste à trouver des paires de premiers
dont l'écart est minimum, inférieur à ce que prévoit le théorème. |
Entre 1 et 9, ils sont 4: 2, 3, 5 et 7 Vers un milliard, il en a 1 tous
les 28 en moyenne. Exemples
de calcul x
= 6 premiers voisins:
5 et 7 écart =
2 log 2 = 1,79 x
= 525 premiers voisins:
523 et 543 écart = 20 log 2 = 6,2 Suite en Comparaison Jumeaux 5 et 7 11 et
13 881 et 883 Écart
moyen E e < E |
||
Voir Tables d'études des écarts
|
|
|||||
|
Écart moitié
Prouvé
en 1965 Écart divisée par 4
Prouvé
en 1988 Écart divisée par une fraction
Prouvé
en 2003 par · Daniel Goldston
(San José) ·
Cem Yildirim
(Istanbul) Annoncé en avril en Allemagne à la
conférence sur la théorie algorithmique des nombres, dans un article appelé:
" Small Gaps Between Primes" |
Rappel Le fait que les nombres premiers jumeaux sont en
nombre infini est une conjecture. Les théorèmes ci-contre, eux par contre, sont
démontrés. Écart
fractionnaire La découverte a été faite en élargissant le champ
des études non pas seulement aux paires, mais aussi aux séquences
de 3, 4 … nombres premiers "Ces résultats pulvérisent toute une
série de records précédents. C'est un peu comme si quelqu'un courait 1000
mètres en deux minutes" Carl Pomerance ( Bell - Murray hill) Ce résultat est tellement meilleur que ce à
quoi nous nous attendions que j'ai failli croire que nous nous étions trompés
D. Goldston |
||||
|
|
||
|
Conjecture
d'Andrica Pn
et Pn+1 sont deux nombres premiers consécutifs, alors pour
tout n => |
|
|
|
Pour
n jusqu'à un million, cet écart entre racine vaut au maximum 0,671 et elle
est atteinte dès la paire (7, 11). |
|
|
|
Tous
les calculs actuels montrent que => |
= 0,670873479 |
|
|
Ce
tableau montre l'écart entre racines pour le record de distante entre les
deux premiers jusqu'à un million Ex: entre 887 et 907
l'écart est de 20 pour la première fois et la différence entre les racines
est égale à 0,333… La
conjecture a été vérifiée jusqu'à plus de 1016. Avec un écart très nettement inférieur à 1.
Mais, la conjecture n'est pas prouvée. |
|
|
|
En 1992, Baugh et O'Hara découvrent ces deux premiers, séparés par 4 247
unités. |
10314
– 1929 et 10314 + 2318 L'écart
entre racines est de
l'ordre de 2 10-154 |
|
|
Généralisation
de la conjecture d'Andrica. Constante de Smarandache:
plus petit x tel que:
Alors n = 30, Pn = 113 et Pn+1 =
127. Cette la plus petite valeur constatée, mais jamais démontrée. Anglais: the Smarandache constant is the smallest x such that q^x - p^x = 1
for two successive primes p,q. OEIS A038458 |
|
|
|
|
||
|
Les
premiers sont cernés! Soit E est l'écart entre deux nombres premiers: Il
y en a une infinité de nombres premiers tels que: |
||
|
E quelconque |
||
|
E / 2 |
Prouvé
(1965) |
|
|
E / 4 |
Prouvé (1980) |
|
|
E / n |
Prouvé (1980) |
|
|
E = 2 (les jumeaux) |
||
|
|
||
|
DISTANCE entre paires de premiers ·
L'infinité des premiers jumeaux n'est qu'une
conjecture. ·
Cherchons à déterminer l'écart minimum entre deux
premiers consécutifs. Si l'on trouve 2,
la conjecture est prouvée. ·
Mais, l'état des recherches n'en est pas encore là.
Quoiqu'un grand pas vient d'être franchi en 2003. |
pk est le kième nombre
premier pk+1 le suivant L'écart ou distance entre eux est dk = pk+1 - pk dk = 2 pour les premiers jumeaux |
|
|
DISTANCE pour de très grands nombres ·
On s'intéresse aux premiers plus grands qu'un très
grand nombre N: ·
Quelle est la distance la plus petite pour toutes les
paires au-delà de N ? ·
Que se passe-t-il pour N tendant vers l'infini? ·
Comparons la distance minimum avec la distance moyenne: ·
Que devient ce rapport quand N tend vers l'infini? |
Pour tout pk > N Valeur de dkmin ? Si la conjecture sur les jumeaux est vraie: dkmin = 2 pour les paires au-delà de N
aussi grand que l'on veut. Rkmin = dkmin / dkmoyen = dkmin
/ ln pk Si la conjecture sur les jumeaux est vraie: Rkmin = 2 / infini = 0 pour les paires
au-delà de N aussi grand que l'on veut (
Attention, pas réciproque ! ) |
|
|
COURSE AUX RECORDS
|
||
|
DERNIÈRES NOUVELLES Rkmin
= dkmin / ln pk ® 0
En anglais
|
|
|
|||
|
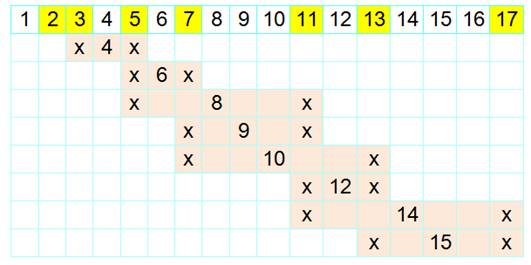
· Un problème amusant consiste à vérifier si un nombre entier quelconque
est entouré de deux premiers avec le même écart de part et d'autre. · La table ci-contre montre que cela est faisable jusqu'à 15. |
|
||
|
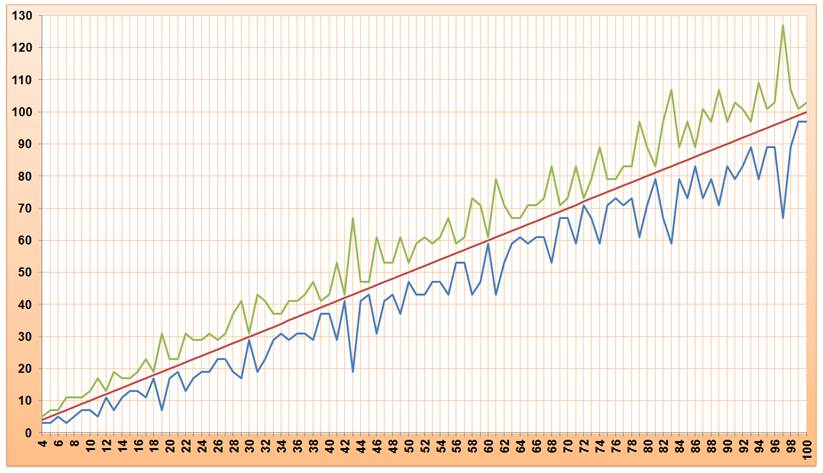
· Ce graphe montre le comportement des nombres de 4 à 100: c'est
toujours faisable avec des écarts plus ou moins grands. · Les valeurs retenues sont celles qui donnent l'écart minimum. Il
existe souvent d'autres possibilités avec des écarts plus grands.
|
|||
|
· Cette propriété n'est pas étrange lorsqu'on sait que la conjecture de Goldbach a été vérifiée
jusqu'à 4 1018 en 2012. · En effet, reprenons notre nombre n
et l'écart e avec les nombres
premiers Pmin et Pmax. n – e = Pmin n + e = Pmax 2n = Pmin
+ Pmax · Les nombres pairs en 2n sont somme de
deux premiers. Ceci est bien l'énoncé
de la conjecture. |
Record
pour e, le plus petit écart pour chaque nombre
|
||
![]()
|
|
||
|
Quels
sont les plus petits nombres premiers tels que l'écart entre lui et son
prédécesseur soit exactement k ? ·
Pour 5, l'écart est de 2
avec 3; ·
Pour 11, l'écart est de 4
avec 7; ·
Pour 29; l'écart est de 6
avec 23; ·
Etc. avec un écart en 2k. |
[2, 5], [4, 11], [6, 29], [8, 97], [10, 149], [12, 211], [14, 127],
[16, 1847], [18, 541], [20, 907], [22, 1151], [24, 1693], [26, 2503], [28,
2999], [30, 4327], [32, 5623], [34, 1361], [36, 9587], [38, 30631], [40,
19373], [42, 16183], [44, 15727], [46, 81509], [48, 28277], [50, 31957] … |
|
|
|
Programme de recherche des premiers avec un écart
donné de plus en plus grand Redémarrage propre et initialisation de la liste
L destinée à recevoir les résultats. Boucle en n, l'écart cherché (il est toujours
pair). Initialisation des deux premiers nombres premiers
p1 et p2. Boucle de recherche des premiers. Calcul de la
différence. Si elle est égale à la consigne n, p2 est placé dans la liste et
on arrête la recherche (break). Préparation des deux nombres premiers suivants. Fin des boucles (od) et impression de la liste. En bleu, résultat de l'exécution. |
|
Voir Programmation – Index
![]()
|
Suite |
|
|
Voir |
·
Nombres premiers – Index
|
|
Aussi |
·
Facteurs premiers autour de 1000 ·
Jumeaux |
|
DicoNombre |
· Nombre
0,567… (Smarandache) · Nombre
0,670 … · Nombre
10314 |
|
Sites |
·
Notes: Goldston & Yildirim's
Result · Generalized Andrica
Conjecture · Andica's
Conjecture – Wolfram Mathworld · Smarandache
Constants – Wolfram Mathworld · Six Conjectures
Which Generalize Or Are Related To Andrica’s Conjecture – Florentin
Smarandache, Ph D (New Mexico) · The Top-20 Prime Gaps
– Jens Kruse Andersen · The Gaps Between Primes –
The Prime Pages'list · The 20 overall merits – Gapcoin –
Jacobsen – 2018 January · Prime gap – Wikipedia · OEIS A005250 – Record gaps between primes |
|
Journal |
· Courrier International du 17 au 23 avril 2003 |
|
Cette page |
![]()