|
|||||||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ par 11,
101, 1001… et par 9, 99, 999 … Critères de divisibilité avec ces
nombres et leurs suites. Si un nombre est divisible par un de
ces nombres, il est aussi divisible par leurs facteurs premiers. En bonus: cas particuliers et
amusants de divisibilité par 99, 99…9 … >>> |
Factorisation de ces nombres

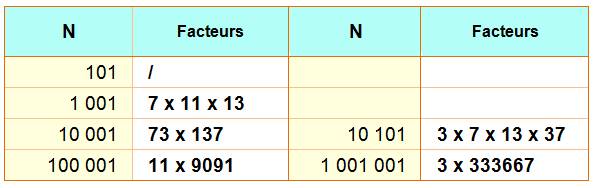
Voir Repdigits
/ Repdigits en 9
|
|
|
|
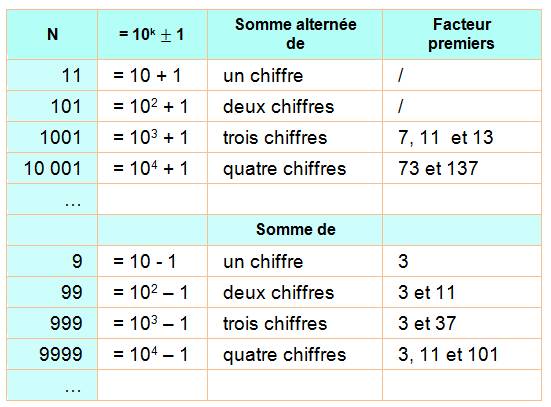
Ces nombres sont proches, à l'unité près, d'une
puissance de 10. Selon cette puissance, le test de divisibilité
s'effectue sur des blocs de mots de taille égale à l'exposant. Par exemple
pour 999 et 1001, on formera des blocs de trois chiffres à partir de la
droite. La somme est directe pour les nombres en 99 … et alternée pour ceux
en 11, 101 … |
|
|
|
||
|
|
123 456 789 |
|
|
|
12 22 21 44 50 16 |
|
|
|
123 332 544 986 666 666 679 13 662 546 |
|
|
|
35 31 |
|
|
|
16 09 50 57 1 48 73 09 52 69 |
|
|
|
123 579 456 3 208 576 527 et 156
= 12 x 13 Divisible que par 13 |
|
|
|
||
|
Pour
les repunits 11, 111 et suivants de n chiffres, tester les blocs
de n chiffres. English: To test for divisibility by 1/9 (10n
– 1) and by its smaller prime factors if any, add the groups of n digits working
from right to left. |
||
|
|
35 31 |
|
|
|
13 703 616 1 184 |
|
|
|
1 3715 9616 |
|
![]()
Cas particuliers de divisibilité
|
|
|||
|
Notez ce motif:
|
|
||
|
Cette propriété se vérifie facilement par l'algèbre => Justifiée également par:
|
N = 10a + b M = 10a' + b' avec a' = 9 – a et b' = 9 – b. N + M = 10a + b + 10(9 – a) + (9 – b) = 10a + b + 90 – 10a +
9 – b = 99 100N + M = 1000a + 100b + 10(9 –
a) + (9 – b) = 1000a + 100b + 90 –
10a + 9 – b =
990a + 99b + 99 = 99 (10a + b + 1) = 99 (N + 1) |
||
|
Florilège |
10 + 89 => 1089 = 99 x 11 11 + 88 => 1188 = 99 x 12 12 + 87 => 1287 = 99 x 13 13 + 86 => 1286 = 99 x 14 18 + 81 => 1881 = 99 x 19 22 + 77 => 2277 = 99 x 23 33 + 66 => 3366 = 99 x 34 34 + 65 => 3465 = 99 x 35 35 + 64 => 3564 = 99 x 36 98 + 01 => 9801 = 99 x 99 8 + 91 => 891 = 99 x 9 |
||
|
Ce même
motif marche avec trois chiffres ou plus. |
123 + 876 =
999 => 123876 =
999 x 124 1234 + 8765 = 9999 => 12348765 = 9999 x 1235 111111888888 = 999999 x 111112 222222777777 = 999999 x 222223 |
||
|
Le
développement algébrique confirme cette propriété. |
N = 1000a + 100b + 10c + d M = 1000(9 – a) + 100(9 – b) + 10(9 – c) + (9 – d) N + M = 9999 10000N + M = 9999 (1000a + 100b + 10c + d + 1) = 9999 (N +
1) |
||
|
Cas général |
|
||
|
Exemple |
123 456 789 876 543 210 = 999 999 999 x 123 456 790 |
||
Voir Calcul
mental – Index
Nombres de quatre chiffres divisibles par 11
|
Trois
chiffres sur quatre sont fixés. Quel
est le quatrième pour que le nombre soit divisible par
11? Exemples 123x
=> 1 + 2 = 4 et 2 + x = 4 => x = 2. En effet: 1232 = 11 x 112 5x26
=> 5 + 2 = 7 et x + 6 = 7 => x = 1. En effet: 5126 = 11 x 466 |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()