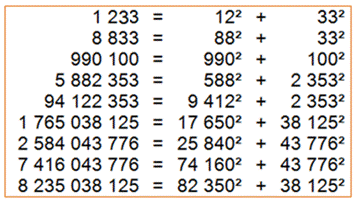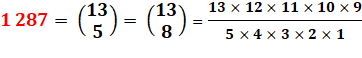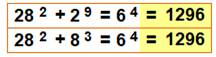NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres	DicoNombre NOMBRES	Glossaire Nombres
1 10 100 500 / 600 700 / 800 900 1 000 1 100	1 200	1 300 / 1 400 1500 / 1900 2000 / 3000 5000 10 000 100 000 10^6 / 10^9 / 10^100
	Mille deux cents ou douze cents Anglais: One thousand and two hundred

1 200

Économie	1 200 $ l'once en 2006 (450 en 2002) pour le platine Plus de 4 millions d'onces (> 100 tonnes) utilisés en 2006 dans le monde pour les pots catalytiques. Une once vaut 28,3495 g Un euro vaut 1, 28 $ (novembre 2006) 1 g de platine vaut en gros 42 $ soit 33 € ou 220 Fr Le platine pour les Espagnols est de l'argent (plata) de qualité inférieure (platina). En France, on l'appelle or blanc ou le huitième élément.	>>>
Sciences	1 200 km distance record en 2017, parcourue par un message codé de manière quantique depuis un satellite avec la Terre, via des lasers. (Chine)	>>>

1 200	Nombre quadrillage
400 = 101² – 99² 800 = 102² – 98² 1200 = 103² – 97² …	Application pour n = 100 de ces identités:
1 201	Nombre carré centré.
	Nombre premier de cette forme en puissance quatrième. Anglais: half-quartan prime. Liste: 41, 313, 353, 1201, 3593, 4481, 7321, 8521, 10601, 14281, 14321, 14593, 21601, 26513, … OEIS A002646
1 206 = 6 × 201	Nombre vampire.
1 207 = 17 × 71 => 1771	Ses facteurs, l'un le retourné de l'autre, forment un palindrome.
1 209 = 3 x 13 x 31	Facteurs amusants. Voir Nombre 2019 et ses permutations
1210 2020	Le plus petit nombre auto-descriptif, et le suivant. Le 1 indique qu'il y a un seul 0 dans ce nombre; Le 2 indique qu'il y a deux 1; Le 1 suivant signifie que le nombre contient un seul 2; et Le 0 final témoigne de la non-présence du 3.
1 210 & 1 184	Deuxième paire amiable.

Géométrie

1210 carrés dans un échiquier (grille) 10 × 10.

>>>

1212 = 12 x 101		Exemple de propriété des nombres blocs: ils sont visibles par le "bloc" (ici: 12).
1212² + 1616² 12012² + 16016² 120012² + 160016²	= 2020² = 20020² = 200020²		Triplets de Pythagore en motifs. Voir 2020
1 215 = 3^5 x 5 1 216 = 26 x 19		Deux nombres successifs avec des puissance 5.
1 215 = 6^4 – 3^4		Nombre binomial.
1 216 = 10^3 + 6^3 = 1000 + 216 = 12^3 – 8^3 = 1728 - 512		Nombre binomial. Deux fois somme de deux cubes avec nombres négatifs autorisés. Voir Table
1 219		Nombre triangulaire centré.
1 221 = 11 x 111		Forme palindrome et repunit. Tous les palindromes à quantité de chiffres paire sont divisibles par 11.

Nombre

1 224 paires de premiers jumeaux jusqu'à 100 000.

>>>

Unité	1 225 km/h = Mach 1 (15°C, altitude 0).	>>>
Jeux	Combien y a-t-il de nombres dont le produit des chiffres vaut 1 225 ? Le chiffre 1 étant exclu car produisant une infinité de solutions. Solution Factorisation de 1225 = 5 x 245 = 5 x 5 x 49 = 5 x 5 x 7 x 7. Si le produit vaut 1 255, ses facteurs à un seul chiffre valent 5, 5, 7, 7. Ce sont les six nombres avec permutation de ces chiffres: 5 577, 5 757, 5 775, 7 755, 7 575, 7 557. En introduisant le chiffre1, il existe une infinité de solutions comme: 15 577, 115 577 … Autre exemple Prenons le nombre 30 = 2 x 3 x 5. Ils sont huit nombres avec un produit de 30, (le chiffre 1 exclu): 56, 65, 235, 253, 325, 352, 523 et 532.	>>>

1 225 = 35² = ½ 49 × 50 = 1 + 2 + … + 49	Nombre triangulaire et carré. Les nombres triangulaires et carrés sont rares: 1, 36, 1225, 41616, 1413721, 48024900, 1631432881, … OEIS A001110
1225: 3, 4, 6, 29, 60, 124, 8c, 9c, 34c, 204c, 408c	Plus petit nombre onze fois polygonal.
1225	Cube évidé à six perforations par côté.
1 225 = T49 = T34 + T35	Triangulaire, somme de nombres triangulaires.
1 225 = 35² = 81 + 82 + …+ 94 = 1^3 + 2^3 + 6^3 + 10^3 = 1^3 + 3^3 + 5^3 + 7^3 + 9^3 = 1^3 + 2^3 + 3^3 + 4^3 + 5^3 + 10^3	Somme d'entiers consécutifs = carré. Carré sommes de cubes Somme des cinq premiers impairs au cube.
1 225 = 35² 1 = 1² et 225 = 15²	Nombre triangulaire qui est également carrément carré.
1 225 = 37² – 12² = 35² = 7² x 5²	Nombre complètement carré.

1 226	Nombre tarte.
1 229	Nombres premiers jusqu'à 10 000.
1 231	Nombre premier pointé.

1233 = 12² + 33²	Les chiffres des deux nombres se retrouvent dans la somme de leurs carrés.
1 233		Motifs avec carré des parties du nombre.

1, 2, 3, 4, 2, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43, 123, 124, 132, 134, 142, 143, 213, 214, 231, 234, 241, 243, 312, 314, 321, 324, 341, 342, 412, 413, 421, 423, 431, 432, 1234, 1243, 1324, 1342, 1423, 1432, 2134, 2143, 2314, 2341, 2413, 2431, 3124, 3142, 3214, 3241, 3412, 3421, 4123, 4132, 4213, 4231, 4312, 4321		Les 64 combinaisons réalisées avec les chiffres d'un nombre à quatre chiffres distincts. Q = 4 + 4·3 + 4·3·2 + 4·3·2·1 = 4 + 12 + 24 + 24 Q = 4 ( 1 + 3(1 + 2(1 + 1(1))))
1 234 = 2 x 617	Les sommes des chiffres deux à deux consécutifs sont des nombres premiers: 1+2 = 3; 2+3 = 5 et 3+4 = 7. Notez que le nombre 1234, n'est pas premier.
1 234 = 1 + 11 + 111 + 1111	Somme des nombres en 1.
1 234 : 1^3 + 2^3 + 3^3 + 4^3 = 100	Somme des chiffres au cube vaut 100 Vrai pour toutes les permutations.
1 234 / 4 = 311, 5	Il n'est pas multiple de 4. Voir Devinette
1 234 x 9 = 11 106 et 1+1+1+0+6 = 9 6 789 x 9 = 61 101	Nombre croissant le plus petit à quatre chiffres. Pour tous les nombres croissants (chiffres de plus en plus grands vers la droite) multiplié par 9, la somme des chiffres est égale à 9. Motif permuté avec le plus grand nombre croissant à quatre chiffres (6789)
1 234 344 fois le chiffre 4 de 1 à 1 234.	Quantité de chiffres 4 pour compter de 1 à 1234: 300 de 1 à 1000 et 44 de 1000 à 1234. Il y en a 4 671 pour aller jusqu'à 12345; 59 053 pour 123456; etc. Statistique
	Nombres à chiffres consécutifs croissants et décroissants Un seul est premier (4567). Presque tous divisibles par un petit facteur. Aucun n'est un carré ou une puissance.

1 237	Le plus petit nombre premier à quatre chiffres dont tous les chiffres vont croissants.
1 237 => 2, 3, 7, 13, 17, 23, 31, 37, 71, 73, 127, 137, 173, 271, 317, 1237, 1327, 1723, 2137, 2371, 2713, 2731, 3217, 3271, 7213, 7321 sont premiers		Nombre multi-premier 26 fois. Primeval.

Histoire	1234 mariage de Louis IX (Saint Louis).	>>>
Histoire Ésotérisme	1244 plutôt que d'abjurer leur foi, 215 personnes se rendent au bûcher dressé au pied du château de Montségur.	>>>

1 241 = 8^3 + 9^3 = 17 x 73	Nombre binomial. Somme de deux cubes de nombres successifs: n^3 + (n+1)^3. Elle est toujours divisible par (2n+1).
1 243 = 11 x 113	Plus petit nombre à quatre chiffres différents divisible par 11. Le plus petit en autorisant le 0 est: 1023.
1 247	Nombre pentagonal.

1 250

1 255 = 5 × 251	Nombre vampire. Nombre dont les chiffres se retrouvent exactement dans ses facteurs.
1 255	Quantité de partitions de 20.
	Nombre dont la somme des diviseurs est égale à la somme des diviseurs de son totient.
1 259	Premier de Bertrand.

1 260 = 2^2 × 3^2 × 5 × 7 = 21 × 60 = 8! / 2^5 = 40 320 / 32	Nombre vampire N°1. Factorielle divisée.
1 260 = 6 × 210	Nombre vampire.
Div(1 260) = [1, 2, 3, 4, 5, 6, 7, 9, 10, 12, 14, 15, 18, 20, 21, 28, 30, 35, 36, 42, 45, 60, 63, 70, 84, 90, 105, 126, 140, 180, 210, 252, 315, 420, 630, 1260]		36 diviseurs: nombre hautement divisible (record de quantité de diviseurs).
1 260 mouvements	Il est possible de mettre le Rubik cube dans une position telle que 1260 mouvements sont nécessaires pour le reconstituer. C'est la valeur maximale.
1 260 jours = 180 semaines	Divisible par 7.
1 260	Hautement brésilien (16 fois).
1 260 = 1.2.3 + 2.3.4 + 3.4.5 + 4.5.6 + 5.6.7 + 6.7.8 + 7.8.9			Somme de produits de nombres consécutifs.
1 260 = 4^3 + 5^3 + 6^3 + 7^3 + 8^3 = 30 x 42			Somme de 5 cubes successifs, toujours divisible par 5n.

1 261	Nombre étoilé.
1 266	Nombre pentagonal centré.
1 266 = 6 × 211	Nombre presque vampire. Factorisation utilisant ses propres chiffres.
1 267 = 3^5 + 4^5	Nombre binomial.

Géométrie

1260° = 7 x 180° Somme des angles de l'ennéagone.

>>>

1 276

Nombre tarte.

1278	Huit permutations sur 24 du nombre 1278 ont douze diviseurs. De plus 12^3 = 1728: nombre égaux au cube de la quantité de diviseurs

Histoire Religion

– 1280 à – 1250 Moïse.

>>>

1 280 = 6^4 – 2^4	Nombre binomial.
1 281	Nombre octogonal (21^e).
1 285 = (1 + 2^8) x 5	Nombre de Friedman.
1 287 = 21 x 87 2 187 = 27 x 81	Nombres de Friedman multiplicatifs et jumeaux
		Coefficient du binôme ou nombre de Pascal.
	Quantité d'issues primitives avec huit dés.
1 287 = 3^3 + 4^3 + 5^3 + 6^3 + 7^3 + 8^3 = 33 x 39	Somme de 6 cubes successifs, toujours divisible par 6n+15.
	Notez ce motif: Les chiffres de 87 sont les compléments à 9 de ceux de 12; La somme est égale à 99 par construction; La concaténation 1287 est un multiple de 99; et Le facteur 13 est égal au nombre choisi plus 1. Règle générale de formation de nombres divisibles par 99 et généralisable aux nombres divisibles par 99…9.

Cosmologie	1292 comètes Observées jusqu'en 1988.	>>>
Jeux	1 296 rectangles dans un jeu d'échecs.	>>>
Graphes	1 296 arbres étiquetés d'ordre 6.	>>>

1 290 = 14² + 15² + 16² + 17² + 18²	Somme de 5 carrés consécutifs, toujours divisible par 5.
1 291	Panconsommable Toujours atteint par k / (somme des chiffres de k) dans toutes les bases.
1 291² = 1 666 681	Carré à chiffres répétés.
12, 92, 104, 196, 300, 496, 796, 1292		Fibodiv: suite de type Fibonacci dont les chiffres en semence engendre le nombre.

Graphes

1 296 arbres étiquetés d'ordre 6. Formule de Cayley: 1296 = 6^6^– 2

>>>

			Fiedman sauvage.
81 = 9² et 8+1 = 9 324 = 18² et 2(3+2+4) = 18 1296 = 36² et 2(1+2+8+6) = 36	Seul nombre carré dont la somme des chiffres est sa racine carrée. Puis, les deux seuls nombres dont la racine carrée est deux fois la somme des chiffres.
1 296 = 36²	Dénombrement des rectangles dans l'échiquier.
1 296 = 6^4 = 36 x 36 = 27 x 48	Un calcul interprété à partir d'un texte de Platon. 12 960 000 = Nombre de Platon.
1 296 divisible par (1, 2, 9, 6)	Nombre de Zuckerman.
1 296 = 6^(9 – 1) / 2 = 6^4 = 1^3 + 2^3 + … + 8^3 = (4 x 9)²	Nombre de Friedman. Nombre de possibilités avec 4 dés. Somme des cubes successifs. Somme de puissances de nombres consécutifs divisible par le nombre suivant - Propriété générale.
1 296 = 36^2 = 6^4 2 916 = 54^2 9 216 = 96^2 9 261= 21^3	Motif avec permutation des chiffres sur quatre nombres, assez rare. Race et Care CARE (soin) est l'anagramme de RACE (course) en anglais En remplaçant les lettres par un codage alphabétique choisi: Si CARE = 1296 = 36² alors RACE = 9216 = 96² Ce qui constitue des anagrammes numériques.
1 296 = 36² = T8^2 = 2^3 + 6^3 + 7^3 + 9^3 = 2^3 + 3^3 + 4^3 + 5^3 + 7^3 + 9^3 = 1^3 + 2^3 + 3^3 + 4^3 + 5^3 + 6^3 + 7^3 + 8^3 = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8)^2		Carré somme de cubes. Somme des cubes successifs de 1 à 8 qui est égale somme au carré des mêmes nombres (propriété générale pour les nombres consécutifs)
		Carré + puissance = puissance.
1 296 = 2 x (1 + 2 + 9 + 6)²		2-digipuissant-carré.
1 296 = 6^4 = 5 x 4^4 + 2^4 = 1280 + 16	Égalité en puissance 4. Illustration du théorème de Mordell-Faltings
–1 296 = (3 + i3)^8 = (3 – i3)^8	Entier = puissance de nombre complexe.

1 299 1+2+9+9 = 21 & 1x2x9x9 = 162

Les chiffres de la somme des chiffres se trouvent dans le produit et dans le nombre lui-même.

Suite	Nombres 1 300
Voir	Nombre Chanceux Semaine Palindrome Triangle Tectroèdre Raisonnement Rep Unit Suites Nombre Têtus
Cette page	http://villemin.gerard.free.fr/NombDico/N1000/N1200.htm

Quelques repères dans ces pages >>> NOMBRE 1 260 Vampires >>> JEU DE DÉS

>>> NOMBRE DE MACH >>> MOISE >>> MONTSÉGUR & LES CATHARES