|
|||||||||||||||||||||||||||||||||||
![]()
|
Partager
un carré en sept carrés en quatre coups de ciseaux. |
|
Dissection des TRIANGLES en 7 Pour commencer, un problème simple
de géométrie impliquant sept triangles
isocèles. Pour suivre, une énigme assez classique: comment partager
le triangle donné en sept
triangles de même aire. Un autre problème classique
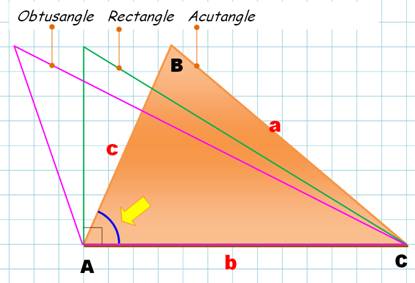
consiste à découper un triangle obtusangles
ou un carré en
un minimum de triangles acutangles. |
Les trois familles de triangles
|
|
|
|
|
|
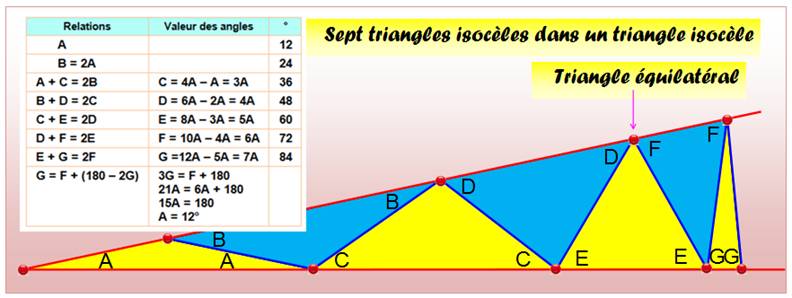
Un
grand triangle isocèle est partagé par sept
triangles isocèles emboités. Déterminer les angles de tous ces triangles
isocèles. Une
affaire qui se conduit d'un bout à l'autre en utilisant la propriété de la somme des angles d'un
triangle. Sans oublier une dernière relation témoignant du fait que le grand
triangle est isocèle.
|
|
|
|
||
|
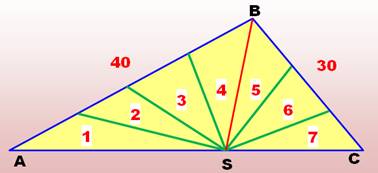
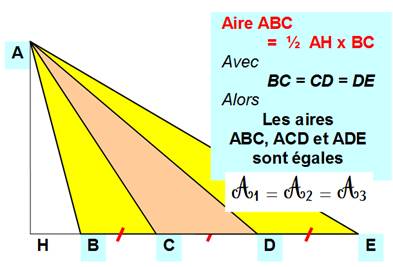
Problème Un
triangle quelconque dont deux des côtés mesurent 40 cm et 30 cm. Comment
s’y prendre pour obtenir sept triangles de même aire ? Où se situe le
point S? |
|
|
|
Indice Des
triangles ayant même hauteur et même longueur de base ont la même aire. Les
hauteurs SH et SH' seront égales si S est sur la bissectrice
de l’angle ABC Les
bases seront de même longueur en découpant des segments de même longueur (10
cm) sur les côtés AB et BC. |
|
|
|
Solution Le
côté de 40 cm est partagé en quatre segments de 10 cm et celui de 30 cm est
partagé également en segments de 10 cm. Les
points de coupure sont les sommets des segments issus de S. Propriété des triangles Le
point S sur la bissectrice partage AC dans le même
rapport que celui entre la longueur des côtés.
Généralisation ? La
solution est ici possible du fait que la longueur des côtés est dans la bonne
proportion (AB / BC = 4/3). |
La
généralisation n’est pas possible. Par contre : - Le
triangle peut être partagé en k parties si les côtés AB et BC peuvent être
partagés en k parties égales ; et - Le
triangle peut alors être quelconque (angle en B quelconque). |
|
|
|
||
|
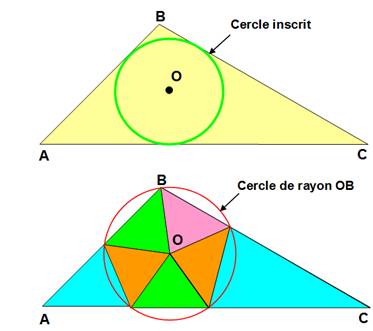
Le
plus petit nombre de triangles acutangles nécessaire pour disséquer un
triangle obtusangle est sept pour C > 90°
et C- A < 90 et C – B < 90; il en faut huit
dans les autres cas. Exemple ici de découpe en
sept triangles isocèles. >>> |
|
|
|
|
||
|
Découper un triangle
quelconque en sept parties égales: il s'agit d'une construction très simple
et qui semble miraculeuse, magique ! Commençons par un rappel sur
le calcul de l'aire du triangle. |
|
|
|
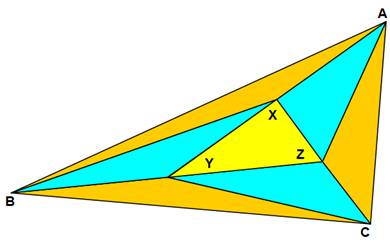
Étape 1 Pour que ce soit
plus facile, on va construire six triangles d’aires égales autour d’un
triangle quelconque XYZ. Le triangle
final ABC sera bien formé de 7 triangles égaux. On commence par prolonger
les côtés par un segment
de même longueur que le côté: AX = XY BY = YZ CZ = ZX |
|
|
|
Étape 1 Les 7 triangles formés ont la même
aire. En effet AXZ et AZC: même hauteur issues
de A et bases égales: XZ = ZC ð même aire YXZ et YZC: même hauteur issue
de Y et bases égales: XZ = ZC ð même aire Idem pout tous les
autres |
Il existe deux
découpages en sept triangles: celui-ci et celui
obtenu en prolongeant les côtés dans l'autre sens. |
|
|
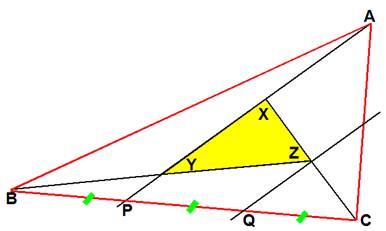
Propriétés Traçons la parallèle ZQ à AY BY = YZ => BP = PQ XZ = ZC => PQ = QC Donc BP = PQ = QC et
AP coupe BC au 1/3 |
A l'instar des
médianes, AP peut être appelée une tritiane *. Il
en existe 6 dans un triangle. *
D'après J.-P.
Boudine |
|
|
Le voyageur indécis A, B et C sont les localités où habitent
trois charmantes jeunes filles. M est un jeune homme qui décide d'aller voir
sa belle. Mais laquelle est-ce? Il se dirige vers Adeline et s'arrête à
mi-chemin et décide d'aller plutôt chez Christine. A mi-chemin, il se souvient que Brigitte
serait plus à son goût. Mais à mi-chemin, etc. |
Depuis M quelconque,
en suivant la règle du mi-chemin, on finit par tourner en rond sur le
triangle du 1/7 intérieur. |
|
|
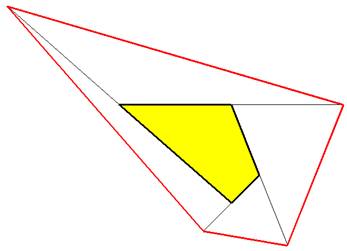
Généralisation Le quadrilatère
extérieur est le "dédoublement" du quadrilatère intérieur. Son aire est égale à 5 fois celle du petit. |
|
|
|
Partager
un carré en sept carrés en quatre coups de ciseaux. Avec
deux coups de ciseaux, le carré initial est partagé en quatre. Avec les deux
suivants, un des petits carrés obtenus est divisé en quatre. Soit 4 – 1 + 4 =
7. Chaque
double coup de ciseaux supplémentaire ajoute trois carrés de plus; que ces
soit dans le carré moyen ou dans le plus petit. On obtiendra toujours 3k + 1
carrés. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/SeptTrg7.htm
|
![]()