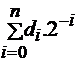|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Il
existe 10 sortes de personnes ceux
qui connaissent le binaire et ceux qui ne le
connaissent pas. |
Voir
Pensées & humour
|
CONVERSION BINAIRE / DÉCIMAL Comment
convertir un nombre exprimé en base 2 (binaire) en un nombre en base 10 (décimale)? |
|
|
||
|
|
Symboles 0 1 Positions Chaque position
successive vers la gauche indique une valeur deux fois plus importante que
celle juste à droite. …. 8
4 2 1 |
|
|
|
|||||||||||||
|
11012 =
1310 Qui se
lit: 1101 en base 2 (binaire) est égal à 13 en base 10 (décimale)
Le 1 à droite "pèse" 1; Le 0 qui suit contribue pour 0; Le 1 ensuite est dans la colonne de
poids 22 = 4, il "pèse" 4; Le 1 final à gauche ajoute 23
= 8; et La somme des poids donne: 1 + 0 + 4
+ 8 = 13 Formulation
|
|||||||||||||
Voir Formation des nombres décimaux en
guise d'introduction
|
|
|||||||||||||
|
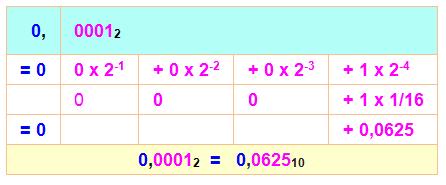
Partie décimale
0,11012 =
0,812510
Le premier 0 à gauche indique que la
partie entière est nulle; Le 1 suivant, juste après la virgule
contribue pour ½ = 0,5; Le 1 qui suit, pèse la moitié du
précédent soit 0,25. En puissance, on
note 1/22 ou avec un exposant
négatif pour éviter la fraction: 2-2; Le 0 suivant n'apporte rien; Le denier 1 à droite contribue pour
1/24 = 1 / 16 = 0,0625; Bilan: 0,5 + 0,25 + 0 + 0,0625 =
0,8125. |
|||||||||||||
Exercices
|
|
|
|
|||||
|
4310 = 1010112
La procédure consiste à diviser le
nombre par 2 et à conserver le reste, puis faire la même chose avec le
quotient. 43 = 2 x 21 + 1, je garde le 1 en
poids fort (chiffre à gauche du nombre binaire) Je continue avec 21 = 2 x 10 + 1,
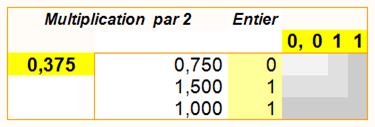
etc. 0,3752 =
0,0112
La procédure consiste à multiplier le
nombre par 2 et à sortir la partie entière (le 1), si elle existe. Ainsi 0,375 x 2 = 0,750: pas de partie entière, le chiffre à
retenir est 0. Étape suivante: 0,750 x 2 = 1,5:
partie entière 1 qui donne le chiffre suivant et que je retire au nombre qui
devient 0,5. Dernière étape: 0, 5 x 2 = 1: donne
1, le chiffre suivant. Retiré du nombre donne 0, ce qui conclut la
conversion. Résultat pour la
somme des deux nombres
Simple addition des résultats |
|||||
![]()
|
|
Voir Maple
|
|
||||
|
Algorithme de conversion décimal en
binaire 1) Mettre le reste de la division par 2 du nombre en cours dans une liste
L. 2) Le nombre suivant est le quotient de la division par 2 du précédent. 3) Répéter ces deux opérations tant que n est plus grand que 0. 4) Imprimer la liste dans l'ordre inverse. |
Exemple 10 => [0], 5 2 => [0, 1, 0], 1 1 => [0, 1, 0, 1], 0 0 => Fin [1, 0, 1, 0] est le binaire
de 10 |
|||
|
Programme Maple
Les
lignes cochées en rouge servent à des vérifications. |
Commentaires Soit un nombre (123)
à convertir en binaire dans la liste L. Pour vérification, conversion directe par
l'instruction existante (convert). Tant que le nombre n
reste plus grand que 0 recommencer ce qui
suit. Dans la liste L,
on ajoute le reste de n divisé par 2 (irem,
integer remainder). Le nombre n
évolue; il prend la valeur du quotient (iquo)
de sa division par 2. En fin de recherche, q
indique la quantité de valeurs enregistrée dans la liste L. L'instruction seq
a pour but d'examiner les éléments de L de
1 à q, en les replaçant en sens inverse. Le point virgule indique que cette liste de
nombres doit être visible. |
|||
|
Programme Python
|
Commentaires On définit une fonction de conversion d'un nombre
décimal en binaire (DB). Le pointeur i permet
d'adresser la liste L pour y ranger le
reste de la division de n par 2 (n % 2
correspond à n mod 2). La boucle en j imprime la liste dans l'ordre
inverse. Le programme principal imprime n et sa conversion
binaire. |
|||
|
Autre méthode à titre d'exercice
(Maple)
Les
instructions cochées en rouge servent à des vérifications. |
Problème posé Soit un entier n = 123. Écrire un algorithme qui
donne la plus grande puissance k de 2 telle que sa valeur ne dépasse pas n. Utiliser
cet algorithme pour écrire n en une somme de puissances de 2. Algorithme mis en procédure Maple Son nom: Test de puissance de 2: Tp2. Première puissance p2 = 0 et premier exposant k =
0: Tant que la puissance de 2 restent inférieure à
n, faire croitre la puissance en incrémentant la valeur de k (k : = k + 1): La condition remplie, la boucle s'interrompt et
la procédure retourne la valeur de l'exposant k. Programme principal Quelles sont les puissances de 2 qui ajoutées
redonnent le nombre n? Celles-ci seront enregistrées dans la liste L. Pour vérification, conversion binaire directe. Tant que le nombre n reste positif, faire ca qui
suit. Retenir l'exposant k qui n'entraine pas un
dépassement de n et soustraire cette puissance de 2 du nombre analysé. En fin de boucle, imprimer la liste L. Pour se rassurer, afficher la liste des valeurs
des puissances de 2 et leur somme. An bleu: le nombre n et sa conversion binaire; puis,
le résultat affiché par le programme: exposant des puissances de 2 conduisant
à la somme n. Puis viennent les valeurs des puissances de 2 et leur somme. |
Voir Programmation – Index
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()