|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CONVERSION en OCTAL B Comment convertir un nombre
exprimé en base 8 (octal) en un nombre en base 10 (décimale) et inversement. En résumé En octal, on compte avec 8
symboles. Le nombre décimal 8 s'écrit
10 en octal.
Intérêt pour nommer plus simplement les nombres
binaires
|
Voir Construction du système décimal
/ Nombre 8 / Brève
325 / Brève
847
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
Additions en octal

Voir Somme en octal
(programmation)
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Quelle est la
valeur du nombre en octal: 4321 ?
Exemple
de lecture: en
4e position (colonne de gauche) qui représente la valeur 83
(= 512), on trouve le chiffre 4 dans le nombre en octal; cette position
"pèse": 4 x 512 = 2 048 en décimal. 4 3218 = 2
25710 Quelques
exemples de conversions
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Programme
Maple Conversion
en base 10 pour disposer des chiffres dans la liste N. Conversion
en octal, placée en Oct. Addition
pondérée des chiffres pour reformer un nombre. Attention, les logiciels donnent les chiffres de droite
à gauche. Voir Programmation – Index |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Merci à Clémentine Vigier
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0, 4321
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
458 en octal
|
458 10 = 712 8 = 111 001 010 2 |
||||||||||||||||||||||||||||||||||||
|
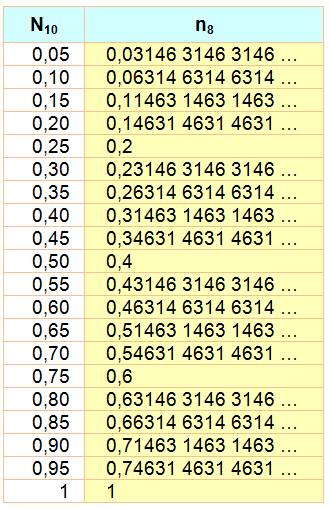
0,458 en octal
|
0,45810 = 0,3528 = 0,011 101 010 012 |
||||||||||||||||||||||||||||||||||||
Exemple
avec disposition pratique: décimal en octal

|
|
||
|
|
On commence par deux procédures qui traitent
séparément la partie entière et la partie décimale. Procédure Décimal-Octal-Entier (DOE) avec entrée
de la partie entière n et de la base b. Boucle de balayage de tous les chiffres du nombre
entier; en fait jusqu'à un quotient (q) nul. Les restes successifs de la division par la base
sont placés dans la liste LL. Les chiffres de celle-ci sont inversés pour
former la liste L des chiffres dans le bon ordre. La procédure Décimal-Octal-Décimal (DOD) avec n
sous la forme0, … On limite la recherche à 30
décimales (par exemple). La partie
entière de la multiplication par la base est placée dans une liste L. Si avant les 30 itérations, le nombre devient
nul, on stoppe le travail en positionnant le compteur d'itérations à 100 (par
exemple). Le programme principal fait appel à
ces deux procédures. Le nombre n et la base sont définis. La partie
entière de n est obtenue en prenant sa valeur plancher (floor). On affiche la concaténation des retours des deux
procédures. Ici, le résultat est donc affiché avec 30
décimales. |
|
|
|
Autre programme principal qui affiche le résultat sous la forme
classique d'un nombre avec décimales. La partie entière est transformée en nombre (nNE)
à partir des chiffres (NE). Idem pour la partie décimale. Les deux nombres sont ajoutés, la partie décimale
étant multipliée par la puissance de 10 négative correspondant à sa quantité
de chiffres. Ce nombre (nbase) est prêt à d'autres usages dans
le programme. |
|
Voir Programmation – Index
Pour info: vous trouverez de nombreux convertisseurs en
ligne sur Internet.
Celui-ci est fourni par RapidTable >>>

|
|
||
|
|
Procédure nommée Soctal: somme de deux nombres exprimés en octal avec
somme en octal. Première conversion: chaque nombre A et B est
transformé en liste de chiffres (mis dans l'ordre inverse). Puis conversion octal vers décimal, toujours en
liste de chiffres. Sommation pondérée par les puissances de 10 pour
restituer les nombres (classiques) en décimal. Addition de A et B en décimal, puis conversion de
la somme en octal. Exemple d'addition de deux nombres en octal, avec
somme en octal. 1 234 5678 + 76 54 3218 = 11 111 1108 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple
avec le nombre binaire 101111010001
Pour information ce nombre vaut 3 025 en
décimal. Cette façon de nommer un nombre binaire est employée en
informatique, car plus compacte que
le binaire, et plus facile à écrire. Cependant, aujourd'hui, l'hexadécimal – regroupement en paquets de quatre bits
– est plus utilisé. Décimales
pointées (ou décimale à points) En informatique de réseaux, les adresses (adresse IP)
sont représentées sous la forme de décimales
pointées. Le code binaire est décomposé en octets, lesquels sont
convertis en décimale. Chacun est séparé par un point. Exemple Binaire: 11000000 10101000 10001000
00011100 Décimales pointées: 192. 168. 136. 28 Adresse IP: 192.168.136.28 Notez les trois"0" pour le nombre 28 en
binaire Notez que le nombre binaire est décomposé en octets,
mais pas codé en octal, mais en décimal. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Ordinateurs / Réseaux
![]()
Voir
Tables
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Numerati/ConOctal.htm
|
![]()