NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 18/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres PREMIERS
Débutants Nombres Premiers	Formules				Glossaire Nombres Premiers
INDEX Nombres premiers – Formules	Formules	n² + n + 41	Tables	Efficacité
	Séquence 31, 24	a . n² + b	R = (2^p – p) p# - 1
		Sommaire de cette page >>> Point de la situation >>> Objet de la recherche >>> Formules vedettes >>> Formules générales >>> Polynômes quadratiques >>> Formule de récurrence >>> Formule de Mills >>> Polynômes pour composés >>> Analyse d'une formule >>> Formule universelle

FORMULES produisant des

nombres premiers

Un rêve !

Euler et Ulam ont trouvé des formules (des polynômes) donnant certains nombres premiers.

Aucune formule simple et surtout pratique ne donne que des nombres premiers.

On a bien p² = 24k + 1 (le carré de tout nombre premier supérieur à 3 est de la forme 24k + 1). Mais, hélas de nombreux nombres de cette forme ne sont pas premiers.

Anglais: Formula for primes

POINT de la situation

En 1772, Euler trouve un polynôme très productif: n(n+1) + 41. En 1798, Legendre propose n(n-1) + 41. Legendre montre qu'une fonction algébrique rationnelle ne peut pas produire que des nombres premiers. En 1752, Goldbach prouve qu'un polynôme à coefficients entiers ne peut pas donner que des premiers pour toutes les valeurs entières. Il existe un polynôme à coefficients entiers et à dix variables qui ne produit que des nombres premiers, mais il s'agit en fait d'un jeu d'équations diophantiennes. Il en existe un autre de degré 25 avec 26 variables qui ne produit que des premiers. Le record est détenu par François Dress et Bernard Landreau (2012) avec 58 premiers successifs pour un polynôme du 6^e degré. Certains polynômes ont été redécouverts dans la compétition Internet : Al Zimmermann’s Programming Contest, Prime Generating Polynomials, organisée par Ed Pegg Jr en juillet 2006.

Objet de la recherche

Les nombres premiers sont sous de la forme en 6n 1. Mais hélas tous les nombres de cette forme ne sont pas premiers. Voir La fameuse barre magique On connait la propension des mathématiciens à caractériser divers types de premiers. Les nombres premiers de Mersenne sont les plus célèbres (P = 2^p – 1), car c'est sous cette forme que l'on connait les plus grands nombres premiers. Concernant la production polynomiale, les mathématiciens se posent deux types de problèmes: le problème n sur n: le polynôme doit délivrer n premiers successifs pour une séquence de n valeurs consécutives de la variable. Record en 2012: n = 45 avec des polynômes quadratiques (2^e degré). n = 58 avec des polynômes de degré supérieur à 2. le problème k sur n: le polynôme produit k premiers pour une séquence de n valeurs consécutives de la variable.

FORMULES vedettes – Polynômes quadratiques
QUATRE FORMULES donnant une grande quantité de nombres premiers La célèbre formule trouvée par Euler en 1772 (n² + n + 41), pourtant très simple, produit une extraordinaire quantité de nombres premiers dont les 40 premiers de la liste. Voir Tables des premiers selon ces formules / Spirale d'Ulam

FORMULES Générales
Quelques expressions qui caractérisent: tous les nombres premiers (et, hélas, aussi des composés), ou certains types de nombres premiers.
Formules	Jusqu'à	Remarque
4n + 1 ou 4n – 1	n > 2	Propriétés générales
6n + 1 ou 6n – 1	n > 3	Propriétés générales
30n + {1, 7, 11, 13, 23, 29)	n > 5	Propriétés générales
(2^n – 2) / n	n < 5	Chine
(2^2)^n + 1	n < 4	Nombre de Fermat
k . 2^n – 1		Premiers de Proth
n . 2^n – 1		Premiers de Woodall
n . 2^n + 1		Premiers de Cullen
n . b^n + 1 (n+2 >b)		Cullen généralisés
Mp = 2^p – 1	avec p premier	Nombre de Mersenne
Polynômes	Voir ci-dessous

Progressions arithmétiques

Suites de nombres premiers en progression arithmétique de la forme a + kb

Pour la première ligne: a = 199 et b = 199. Elle produit dix nombres premiers.

Avec a et b jusqu'à 10 000, la suite ne dépasse pas 10 nombres.

17, 6930, [17, 6947, 13877, 20807, 27737, 34667, 41597, 48527, 55457], 9

137, 7980, [137, 8117, 16097, 24077, 32057, 40037, 48017, 55997, 63977], 9

199, 210, [199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879, 2089], 10

221, 6930, [221, 7151, 14081, 21011, 27941, 34871, 41801, 48731, 55661, 62591], 10

409, 210, [409, 619, 829, 1039, 1249, 1459, 1669, 1879, 2089], 9

433, 3150, [433, 3583, 6733, 9883, 13033, 16183, 19333, 22483, 25633], 9

521, 9660, [521, 10181, 19841, 29501, 39161, 48821, 58481, 68141, 77801], 9

583, 8820, [583, 9403, 18223, 27043, 35863, 44683, 53503, 62323, 71143], 9

671, 210, [671, 881, 1091, 1301, 1511, 1721, 1931, 2141, 2351], 9

737, 6720, [737, 7457, 14177, 20897, 27617, 34337, 41057, 47777, 54497], 9

803, 1260, [803, 2063, 3323, 4583, 5843, 7103, 8363, 9623, 10883, 12143], 10

803, 1890, [803, 2693, 4583, 6473, 8363, 10253, 12143, 14033, 15923], 9

937, 9240, [937, 10177, 19417, 28657, 37897, 47137, 56377, 65617, 74857], 9

1007, 630, [1007, 1637, 2267, 2897, 3527, 4157, 4787, 5417, 6047], 9

1513, 2310, [1513, 3823, 6133, 8443, 10753, 13063, 15373, 17683, 19993, 22303], 10

1699, 3990, [1699, 5689, 9679, 13669, 17659, 21649, 25639, 29629, 33619], 9

1807, 4620, [1807, 6427, 11047, 15667, 20287, 24907, 29527, 34147, 38767], 9

1819, 420, [1819, 2239, 2659, 3079, 3499, 3919, 4339, 4759, 5179], 9

1991, 2730, [1991, 4721, 7451, 10181, 12911, 15641, 18371, 21101, 23831, 26561], 10

2057, 9030, [2057, 11087, 20117, 29147, 38177, 47207, 56237, 65267, 74297], 9

2063, 1260, [2063, 3323, 4583, 5843, 7103, 8363, 9623, 10883, 12143], 9

2893, 2520, [2893, 5413, 7933, 10453, 12973, 15493, 18013, 20533, 23053], 9

3211, 3360, [3211, 6571, 9931, 13291, 16651, 20011, 23371, 26731, 30091], 9

3247, 2310, [3247, 5557, 7867, 10177, 12487, 14797, 17107, 19417, 21727], 9

3289, 210, [3289, 3499, 3709, 3919, 4129, 4339, 4549, 4759, 4969, 5179], 10

3413, 5250, [3413, 8663, 13913, 19163, 24413, 29663, 34913, 40163, 45413], 9

3499, 210, [3499, 3709, 3919, 4129, 4339, 4549, 4759, 4969, 5179], 9

3823, 2310, [3823, 6133, 8443, 10753, 13063, 15373, 17683, 19993, 22303], 9

4091, 7980, [4091, 12071, 20051, 28031, 36011, 43991, 51971, 59951, 67931], 9

4589, 2520, [4589, 7109, 9629, 12149, 14669, 17189, 19709, 22229, 24749], 9

4721, 2730, [4721, 7451, 10181, 12911, 15641, 18371, 21101, 23831, 26561], 9

4727, 3150, [4727, 7877, 11027, 14177, 17327, 20477, 23627, 26777, 29927], 9

4841, 4620, [4841, 9461, 14081, 18701, 23321, 27941, 32561, 37181, 41801], 9

5203, 840, [5203, 6043, 6883, 7723, 8563, 9403, 10243, 11083, 11923, 12763], 10

5401, 3570, [5401, 8971, 12541, 16111, 19681, 23251, 26821, 30391, 33961], 9

5543, 2310, [5543, 7853, 10163, 12473, 14783, 17093, 19403, 21713, 24023], 9

5681, 3360, [5681, 9041, 12401, 15761, 19121, 22481, 25841, 29201, 32561], 9

6043, 840, [6043, 6883, 7723, 8563, 9403, 10243, 11083, 11923, 12763], 9

6149, 6090, [6149, 12239, 18329, 24419, 30509, 36599, 42689, 48779, 54869], 9

6493, 2940, [6493, 9433, 12373, 15313, 18253, 21193, 24133, 27073, 30013], 9

6539, 6930, [6539, 13469, 20399, 27329, 34259, 41189, 48119, 55049, 61979, 68909], 10

6553, 7770, [6553, 14323, 22093, 29863, 37633, 45403, 53173, 60943, 68713], 9

6721, 1470, [6721, 8191, 9661, 11131, 12601, 14071, 15541, 17011, 18481], 9

6859, 3570, [6859, 10429, 13999, 17569, 21139, 24709, 28279, 31849, 35419], 9

7151, 6930, [7151, 14081, 21011, 27941, 34871, 41801, 48731, 55661, 62591], 9

7631, 2310, [7631, 9941, 12251, 14561, 16871, 19181, 21491, 23801, 26111], 9

7787, 1050, [7787, 8837, 9887, 10937, 11987, 13037, 14087, 15137, 16187], 9

8347, 4200, [8347, 12547, 16747, 20947, 25147, 29347, 33547, 37747, 41947, 46147], 10

8437, 5040, [8437, 13477, 18517, 23557, 28597, 33637, 38677, 43717, 48757], 9

8483, 4830, [8483, 13313, 18143, 22973, 27803, 32633, 37463, 42293, 47123], 9

8987, 2940, [8987, 11927, 14867, 17807, 20747, 23687, 26627, 29567, 32507, 35447], 10

9557, 6930, [9557, 16487, 23417, 30347, 37277, 44207, 51137, 58067, 64997], 9

9581, 1680, [9581, 11261, 12941, 14621, 16301, 17981, 19661, 21341, 23021], 9

9823, 420, [9823, 10243, 10663, 11083, 11503, 11923, 12343, 12763, 13183], 9

9911, 5040, [9911, 14951, 19991, 25031, 30071, 35111, 40151, 45191, 50231], 9

POLYNÔMES QUADRATIQUES
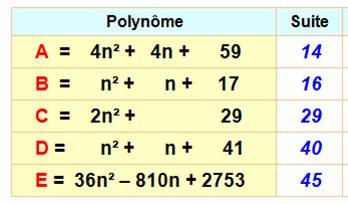
Polynômes du deuxième ou troisième degré qui produisent des nombres premiers successifs. Ex: pour n de 0 jusqu'à 13, le polynôme 4n² + 4n + 59 produits 14 premiers distincts. Le graphe de ces polynômes est une parabole, alors on peut retrouver la même valeur pour deux valeurs différentes de n.
Polynôme				Jusqu'à / Distinct	Auteur / Remarque	Lien
n^3 +	n^2		+ 17	10 / 11
	2n^2		+ 11	10 / 11
	4n^2	+ 4n	+ 59	13 / 14	Honaker Rendement: 0,437 jusqu'à 10 millions
	n^2	+ n	+ 17	15 / 16	Legendre
	3n^2	+ 39n	+ 37	17 / 18	A. Bruno (pers. comm., 2009)
n^4	+ 29 n^2		+ 101	19 / 20	E. Pegg, Jr. (pers. comm., 2005)
	7n^2	– 371n	+ 4 871	23 / 24	F. Gobbo (pers. comm., 2005)
	n^2	+ 3n	– 167	23 / 24	Marius Coman (2012) 42 premiers ente 0 et 46
	n^2	– 49n	+ 431	23 / 24	Marius Coman (2012) Idem à celle en - 167, mais dans l'ordre inverse
	13n^2	– 331n	+ 1 847	23 / 24	Marius Coman (2012)
	13n^2	– 469n	+ 4 217	23 / 24	Marius Coman (2012)
	41n²	– 935n	+ 5557	24 / 24	Louis-Marie Genet
	2n^2		+ 29	28 / 29	Legendre (1798)
	16n^2	– 300n	+ 1 447	30	Marius Coman
	16n^2	– 628n	+ 6 203	36	Idem à celui en 1447, mais en ordre inverse
	8n^2	+ 8n	+ 197	32 / 31	Marius Coman
	16n^2	– 292n	+ 1 373	32 / 31	Marius Coman
	16n^2	– 668n	+ 7 013	32 / 31	Idem à celle en 1 373, mais en ordre inverse
	25n^2	– 1 185n	+ 14 083	33 / 32	Marius Coman
	25n^2	– 365n	+ 1 373	33 / 32	Idem à celle en 14 083, mais en ordre inverse
	81n^2	– 2 247n	+ 15 383	34 / 33	Marius Coman
	81n^2	– 2 937n	+ 26 423	34 / 33	Idem à celle en 15 383, mais en ordre inverse
	4n^2	– 2 247n	+ 15 383	34 / 33	Marius Coman
	4n^2	+ 12n	– 1 583	36 / 35	Marius Coman
	4n^2	– 284n	+ 3 449	36 / 35	Idem à celle en – 1 583, mais en ordre inverse
	4n^2	– 152n	+ 1 607	/ 40	Marius Coman
	6n^2	– 342n	+ 4 903	57 / 29	J. Brox (pers. comm., 2006)	>>>
	6n²	+ 6n	+ 31	30 / 30	Idem ci-dessus sans doublons.	>>>
	8n^2	– 488n	+ 7 243	61 / 31	F. Gobbo (pers. comm., 2005)
	43n^2	– 537n	+ 2 971	34 / 35	J. Brox (pers. comm., 2006)
42n^3	+ 270n^2	– 26 436n	+ 250 703	39 / 40	Wroblewski and Meyrignac
	n^2	+ n	+ 41	40 / 40	Euler, 1772 Rendement: 0,475 jusqu'à 10 millions	>>>
	n^2	– 79n	+ 1 601	40 / 40	Excott Idem Euler avec n n – 40	>>>
	103n^2	– 4 707n	+ 50 383	/ 43	Speiser (pers. comm., 2005)
	103n^2	+ 31n	– 3 391	/ 43	Ruby
	47n^2	– 1701n	+ 10 181	/ 43	Fung and Ruby
	47n^2	+ 9n	– 5 209	-22 à 18 /43	Fung
	36n^2	+ 18n	– 1 801	-33 à 11 / 45	Ruby (1989) – Le record

POLYNÔMES de degré > 2
Alors que la quantité de premiers consécutifs semble plafonner autour de 45 avec les polynômes quadratiques, les mathématiciens ont trouvé des suites de premiers plus longues en recourant aux degrés élevés (jusqu'à 6 actuellement).
Polynôme							Jusqu'à / Distinct	Auteur / Remarque	Lien
3n^3	+ 183n^2		– 3 318n		– 18 757		46 / 43	S. M. Ruiz (pers. comm., 2005)
	36n^2		– 810n		+ 2 753		44 / 45	Fung and Ruby (1989)
– 66n^3	+ 3 845n^2		– 6 0897n		– 25 1831		45 / 46	Kazmenko and Trofimov (2006)
n^5 – 99n^4+ 3 588n^3 – 56 822n^2 + 348 272n – 286 397							46 / 47	Wroblewski and Meyrignac (2006)
6n^3		+ 83n^2		– 13 735n		+ 30 139	-26 à 19 /46	Dress et Landreau
n^4 – 97n^3 + 3 294n^2 – 45 458n – 213 589							49 / 49	Beyleveld (2006)
							/ 49	Dress et Landreau J. Wroblewski et J.-C. Meyrignac
							/ 49	Dress et Landreau
1/4 (n^5 – 133n^4+ 6 729n^3 – 158 379n^2 + 1 720 294n + 6 823 316)							56 / 57	Dress and Landreau (2002), Gupta (2006)
							/ 57	Dress et Landreau Shyam Sunder Gupta
1/36 (n^6 – 126n^5 + 6 217n^4 – 153 066n^3 + 1 987 786n^2 – 13 055 316n + 34 747 236)							54 / 55	Wroblewski and Meyrignac (2006)
							/ 57	Dress et Landreau
							/ 57	Dress et Landreau
							-25 à 31 / 58	Dress and Landreau (2010)	>>>

Autres POLYNÔMES – Premiers dans la plage (mais pas tous)
Ces polynômes produisent des nombres premiers en grandes quantité, mais pas forcément consécutifs. NB. Ce classement mériterait une vérification que je n'ai pas encore effectuée.
Polynôme				Jusqu'à / Distinct	Auteur / Remarque	Lien
	n^2	+ 3n	– 167	46 / 42	Marius Coman
	n^2	– 49n	+ 431	46 / 42	Idem à celui en - 167, mais en ordre inverse.
	2n^2	+ 4n	+ 117		Ulam / Stein / Wells Rendement: 0,05 jusqu'à 10 millions
	n^2	+ n	+ 1		Ulam / Stein / Wells Rendement: 0,29 jusqu'à 300 000
	36n^2	+ 18n	– 1 801	50 /49	Dress et Olivier (1999)
	2n^2	– 212n	+ 5 419	99 / 57	Marius Coman
	4n^2	– 284n	+ 3 449	95 / 60	Marius Coman
	4n^2	+ 12n	– 15 83	95 / 60	Idem à celui en 3 449, mais en ordre inverse.
	2n^2	– 108n	+ 1 259	101 / 66	Marius Coman
	4n^2	– 482n	+ 14 561	99 / 88	Marius Coman (2012)
	41n^2	– 4 641n	+ 88 007	100 / 90	Boston et Greenwood (1995)
	41n^2	+ 33n	– 43 321		Idem à celui en 88 007
	n^2	– 69n	+ 1 231		Euler pour n = m – 35
	9n^2	+ 3n	– 16 229	200 / 166	Dress et Olivier
	n^2	+ n	– 1 354 363	1000 / 698	Dress et Olivier
	4n^2	+ 170n	+ 1 847	1560 / 727	Ulam / Stein / Wells Rendement: 0,466 jusqu'à 10 millions Forme cousine de celle d'Euler avec n 2n + 42	>>>
	n^3 + n^2	– 468 610 n	+ 4 021	1000 / 601	Dress et Landreau
				1000 / 539	Dress et Landreau

Tables d'après: Prime-Generating Polynomial – MathWorld--A Wolfram Web Resource.

A Visual Display of Some Properties of the Distribution of Primes

Ten prime generaing quadratic polynomial – Marius Coman

Polynômes prenant beaucoup de valeurs premières

Sloane A212325 / Sloane A213810

Dress et Landreau

François Dress est professeur émérite en mathématique à l’université de Bordeaux.	Bernard Landreau est maître de conférences à l’université d’Angers.
Record en 2010 avec un polynôme produisant 58 premiers consécutifs. Six mois de calcul avec une quarantaine de processeurs en parallèle du Centre de Calcul Intensif des Pays de Loire et du CNRS. Test de plus de 300 milliards de milliards de polynômes.

Formule de récurrence
La formule suivante engendre des nombres premiers: En commençant avec a1 = 7. Le terme en PGCD est égal soit à 1, soit à un nombre premier. Formule découverte en 2003 par Matthew Frank Démontrée en 2008 par Eric Rowland (université Rutgers aux États-Unis). Exemples Extrait de: a simple prime-generating recurrence – Eric Rowland

Formule de Mills

En 1947, W. Mills propose une formule qui donne des nombres premiers à condition de connaître une constante A. Mais là est le problème: il faut déterminer la constante A, et pour la connaitre avec la précision suffisante, il faut connaître les nombres premiers. Formule de Wills Les crochets désigne la parie entière. Et la constante de Mills vaut: 1,3063778838 6308069046 8614492602 6057129167 8458515671 3644368053 759966434 ...

POLYNÔMES qui évitent les premiers
L'intérêt premier consiste, bien sûr, à se concentrer sur ces individus particuliers que sont les nombres premiers. Mais, certains ont cherché des polynômes qui produisent de longues séquences de nombres composés. NB. On sait, par ailleurs, trouver des séquences de nombres composés aussi longue que l'on veut.
N = 2x – 1 + 4y (x + y) Cette formule engendre quantité de nombres composés, mais sans les donner tous (évidemment); même pas pour les k premiers nombres, par exemple. La table donne toutes les valeurs possibles pour N de 1 à 105. Pour x de 1 à 10 000 et y de 1 à 10 000, toutes les valeurs de N sont composées. Alors N = 800 019 999 = 3^4 .7 .11 .101 .127.

Merci à Christophe pour son aide à la mise à jour de ces pages

Analyse de la formule
Un exemple de formule et recherches associées. Exemple Les quatre premières valeurs sont des nombres premiers: kts = 4. Un test jusqu'à n = 20, montre qu'il y a 11 nombres premiers (kt = 20).
Analyse Pour a de 2 à 20; k de 2 à 20 et n de 1 à 50 kts est la quantité de premiers qui se succèdent depuis le début et kt est la quantité totale sur la plage. La formule en 2 x 6^n + 1 est la plus performante avec 4 premiers qui se suivent et 11 premiers parmi les 20 nombres (exemple vu ci-dessus). La formule en 20 x 3^n + 1 donne cinq premiers de suite. En prenant le signe moins: 2 x 6^n – 1 La formule en 2 x 6n – 1 est plus performante que celle avec les signe plus avec 5 premiers qui se suivent et 13 premiers parmi les 20 nombres.		Signe positif a, k, kts, kt 2, 6, 4, 11 10, 15, 4, 9 20, 3, 5, 10 Signe négatif 2, 6, 5, 13 3, 2, 4, 11 10, 3, 4, 14 12, 6, 4, 12 12, 11, 4, 9

Merci à Cyril N. C.

Formule universelle

Il existe des formules comportant plusieurs variables pour lesquelles, si la valeur de la formule est positive, elle est première.

Il y en a même pour lesquelles chaque nombre premier peut être trouvé comme valeur de la formule pour un ensemble de valeurs positives des variables.

Une telle formule a été trouvée par J.P. Jones, Hideo Wada, Daihachiro Sato et Douglas Wiens, et publiée en 1976 :

(k+2){ 1 - [wz+h+j-q]²
   - [(gk+2g+k+1)(h+j) + h - z]²
   - [2n+p+q+z-e]²
   - [16(k+1)³(k+2)(n+1)² + 1 - f²]²
   - [e³(e+2)(a+1)² + 1 - o²]²
   - [(a²-1)y² + 1 - x²]²
   - [16r²y⁴(a²-1) + 1 - u²]²
   - [((a + u²(u²-a))² - 1) (n+4dy)² + 1 - (x+cu)²]²
   - [n+l+v-y]² - [(a²-1)l² + 1 - m²]²
   - [ai+k+1-l-i]²
   - [p + l(a-n-1) + b(2an+2a-n²-2n-2) - m]²
   - [q + y(a-p-1) + s(2ap+2a-p²-2p-2) - x]²
   - [z + pl(a-p) + t(2ap-p²-1) - pm]² }

Elle comporte 26 variables (de a à z) et son degré est de 25 (car une fois développée, il existe un terme 16d⁴k¹u¹⁶y⁴ dans lequel la somme des exposants est de 25).

Le nombre de variables pourrait être réduit à 10, mais cela nécessiterait d'augmenter massivement la taille des exposants (peut-être jusqu'à 1,6 × 10⁴⁵ — montré par J.P. Jones en 1982).

Source: Robert Mufano

Suite	Formule d'Euler en 41 Tables des nombres premiers selon ces formules Nombre premiers – Index
Voir	Barre magique des nombres premiers Efficacité de ces formules Identités remarquables Liste de nombres premiers Spirale d'Ulam
DicoNombre	Nombre 1,306 …
Sites	Formules pour les nombres premiers – Jean-Paul Delahaye Formules et nombres premiers – CNRS info Formules pour les nombres premiers – Wikipédia Polynômes prenant beaucoup de valeurs premières – François Dress et Bernard Landreau Prime formula – Eric Weisstein Prime-Generating Polynomial – Wolfram MathWorld A Natural Prime-Generating Recurrence – Eric Rowland – 2008 Base-independent classifications of prime numbers – OEIS – Prime numbers by form, in quadratic progression, … Il fascino dei numeri primi – Vittorio Ornago – Recherche de formules produisant des nombres premiers Numeri primi - Sequenze e formule polinominali – Vittorio Ornago – Suite
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Premier/formule.htm