|
||||||||||||||||||||||||||||
![]()
|
RACINE de DEUX est un nombre IRRATIONNEL |
|
|
On disait incommensurable
car il n'y a pas d'unité qui puisse mesurer à la fois 1 et |
Comment démontrer que
racine de deux est irrationnel?
Démonstration par
l'absurde: P et Q devraient être pairs
à la fois … |
Irrationnels
qui produisent du rationnel !
|
|
Voir Racines à
étages
|
Pythagore (–570 à –490) savait
que Theodore de Cyrène (–465 à –398)
a prouvé que la racine carrée des nombres de 3 à 17 est irrationnelle, sauf
pour 4, 9 et 16. |
|
|
||
|
Raisonnons
par l'absurde et supposons |
||
|
Étant
rationnel, on peut l'écrire sous forme d'une fraction |
|
|
|
On réduit
la fraction au maximum |
|
|
|
M et N
n'ont pas de diviseurs en commun |
M et N premiers entre eux |
|
|
Élevons au
carré |
2 = M² /N² |
|
|
Ou |
M² = 2 N² |
|
|
Avec ce
facteur 2, on déduit que |
M² est pair |
|
|
Or, un
nombre élevé au carré, garde sa parité et réciproquement |
M est pair |
|
|
Écrivons
que M est pair |
M = 2K |
|
|
On revient
à l'expression au carré |
M² = 2 N² = (2 K)² = 4 K² |
|
|
Ou, en
divisant par deux de chaque côté |
N² = 2 K² |
|
|
Même
raisonnement sur la parité avec N |
N est pair et N = 2
J |
|
|
Alors M et
N ont un facteur commun |
2 est
facteur commun à M et N |
|
|
La contradiction
montre que l'hypothèse est |
Fausse au départ |
|
|
Et que |
|
|
|
|
|
|
|
Raisonnons
par l'absurde et supposons |
||
|
Fraction
réduite au maximum |
|
|
|
Cette fr Elle est
irréductible |
|
|
|
Seules
possibilités Cf. Fr |
M² = 2 N² = 1 |
|
|
Or |
M² |
|
|
Contr |
|
|
|
|
||
|
Raisonnons
par l’absurde et supposons |
||
|
Fraction réduite au maximum |
|
|
|
Ce nombre
est un entier |
|
|
|
Inégalités |
|
|
|
Multiplication
par racine de 2 |
|
|
|
Selon
notre hypothèse ce nombre est un entier |
|
|
|
Rappel
pour N |
|
|
|
Contr |
|
|
|
|
|
||
|
Exprimons
la racine de 2 sous cette forme |
|
||
|
Ou plus
généralement, si rationnel |
|
||
|
Inégalités |
|
||
|
Dénominateur
de racine de 2 < q qui montre que q n’est pas la valeur minimale |
|
||
|
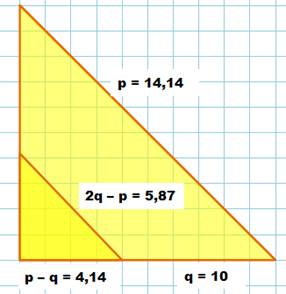
Formulation qui est propice à une
représentation géométrique avec un triangle isocèle
rectangle de côté p et q puis un triangle homothétique de côté 2q – p et
p – q. On amorce alors une descente infinie de
Fermat en poursuivant la construction sans fin en répétant le procédé. |
|
||
|
Autre illustration de la descente infinie
avec des rectangles.
Même proportion longueur sur largeur:
En reconduisant le procédé, nous nous
trouvons face à une nouvelle descente infinie. |
|
||
|
|
||
|
Formule de Héron Voir la
formule |
Tous les termes de cette suite sont rationnels alors qu'elle converge
vers une limite
irrationnelle. |
|
|
Limite de la suite |
En effet:
|
|
|
|
||
|
x² = 2
n'a pas de solution en p-adiques. Or les
nombres les rationnels sont un sous-ensemble des p-adiques. Alors x²
= 2 n'a pas non plus de solution en nombres rationnels. Une
preuve rapide que racine de 2 est irrationnel. |
Preuve en prenant la valuation de chaque côté de
l'égalité. |
|
![]()
Généralisation
|
|
|
|
La
démonstration est un peu longue, car menée pas à pas. Pour
mieux apprécier et soulager l'effort d'abstraction, une indication numérique
est donnée à droite. |
|
|
PREMIÈRE
ÉTAPE: hypothèse conduisant à une équation
caractéristique et unique |
||
|
Soit N un
entier non carré |
N |
N
= 1000 (exemple) √1000
= 31,622… |
|
Si
la racine de N est rationnelle, il existe
une fraction Telle que
p et q n'ont pas de diviseurs communs Ce qui
veut dire que cette forme réduite de la fraction est unique |
p = q . |
√N
≈ 95/3 = 31,66… Une
approximation évidemment. On
ne peut pas simplifier davantage la fraction. |
|
Nous
aurons besoin de la valeur de p. Notons-la
tout de suite |
p = q. |
95
≈ 3 x 31, 622 = 94, 866 |
|
Au carré |
p² = q².N |
95²
= 9025 ≈
3² x 1000 = 9000 |
|
Et mis en
équation Cette
forme étant unique selon notre
hypothèse, Nous allons
montrer qu'il existe deux autres nombres conduisant à une seconde expression
de ce genre. Ce qui sera contraire à notre hypothèse. La contradiction
permettra de conclure que cette hypothèse est fausse |
p² – N.q² = 0 |
95²
- 1000 x 3² = 25 ≈ 0 Toujours
en approximation |
|
DEUXIÈME
ÉTAPE: introduction du nombre juste inférieur à
la racine carrée |
||
|
Il existe
un nombre n tel que |
n < –𝐍 |
31
< 31,622 |
|
TROISIÈME
ÉTAPE: choix de deux nouveaux nombres, en utilisant
la différence entre la racine et son entier inférieur |
||
|
Choix des
deux nombres qui vont soulever la contradiction. Nous allons passer dans le monde des écarts
entre la racine de N et le nombre n juste inférieur. |
||
|
Premier nombre |
p' |
|
|
Écrivons
la valeur de N en produit de fractions Et
remplaçons p/q par une valeur plus petite, n |
N = (p/q) (p/q) N > (n)
(p/q) |
1000 ≈
(95/3)(95/3) 1000 > 31 (95/3)
= 981,6 |
|
En multipliant par q |
N.q > n.p |
1000
x 3 >31 x 95 3000
> 2945 |
|
Notre
premier nombre sera la différence positive issue de cette inégalité |
p' = N.q – n.p |
3000
– 2945 = 55 |
|
Deuxième nombre |
q' |
|
|
Évaluons
l'excès positif entre la racine et le
nombre entier inférieur |
|
31,622
– 31 = 0, 622 |
|
Ou en
remplaçant racine de N par sa valeur supposée
rationnelle |
p/q – n > 0 |
95
/ 3 – 31 = 0, 666 |
|
En
multipliant par q |
p – n.q > 0 |
95
– 31 x 3 = 2 |
|
Notre
deuxième nombre sera cette différence |
q' = p – n.q |
|
|
Bilan: nos
deux nombres sont là |
p' = N.q - n.p q' = p – n.q |
55 2 |
|
QUATRIÈME
ÉTAPE: utilisation des deux nouveaux nombres
pour soulever une contradiction qui montre que l'hypothèse de départ est
erronée |
|
|
Revenons à
l'expression avec les carrés On se souvient
que cette expression est unique du fait de notre hypothèse: p/q est
irréductible |
p² – Nq² = 0 |
|
Calculons
la même chose avec nos deux nouveaux nombres: p' et q' |
p'² – Nq'² = ? |
|
En
remplaçant par les valeurs Et en
procédant au calcul |
(N.q – n.p)² – N (p – n.q)² = N²q² – 2Nnpq
+n²p² – N(p² – 2npq + n²q²) = N²q² + n²p² – Np²
– Nn²q² = N (Nq² – p²) +n²
(p² – Nq²) = (n² – N) (p² – Nq²) |
|
Bilan |
p'² – Nq'² = (n² –
N) (p² – Nq²) |
|
Mais le
deuxième terme est nul. L'expression
complète est nulle |
p'² – Nq'² = 0 |
|
L'expression
n'est pas unique Ce qui
contredit notre hypothèse |
La racine carrée
d'un nombre non carré parfait est un nombre irrationnel. |
|
|
|
|
Racine carrée
Pour tout n appartenant à l’ensemble des
nombres entiers (Z+ = N = {1, 2, 3 …}), la racine carrée de n est
rationnelles que si, et seulement si, n est un carré parfait N². Racine kième
K est un nombre entier supérieur à 2.
Alors, la racine kième de n est irrationnelle, sauf si n est une puissance
parfaire, n = Nk. La racine énième
d’un nombre entier positif, si elle n’est pas un entier, elle est un
nombre irrationnel. Racine évidente d’un
polynôme (Rational Roots Theorem) Ce théorème se
démontre à partir des résultats cités ci-dessus.
Si an et a0 sont des entiers non
nuls, et si une fraction irréductible p/q est racine du polynôme, alors p
divise a0 et q divise an. Voir Suite et exemples |
|
|
Sommes
d'irrationnels En
revanche, Qu'en
est-il de Démonstration par contradiction: on suppose n rationnel.
D'un côté
de l'égalité, on a un irrationnel et de l'autre un rationnel Contradiction
! La somme n est irrationnelle. Pour
information
Voir DicoNombre 1,
41 / DicoNombre
1,73 / DicoNombre
5,59 |
Voir Brève
48-947
|
|
|
|
How do
we know that square root of 2 is an irrational
number? In
other words, how do we know that √2 wouldn't have a pattern in the
decimal sequence? Maybe
the pattern is very well hidden and is really long, billions of digits?
Even if
you check it till million first digits, maybe the pattern is just longer than
you were able to print the digits out with your computer? Here is
where mathematical proof comes in. The
proof that √2 is indeed irrational isn't that difficult to
follow. It
relies on a proof by contradiction.
Then we
can write it √2 = a/b where a, b are whole numbers.
|
|
Voir Anglais – Le bagage minimum
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()