|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Observation sur les multiples de Pi comme approche au Théorème de Dirichlet Quels sont les multiples de Pi qui s'approchent le plus près d'un entier? |
|
|
||
|
|
k k
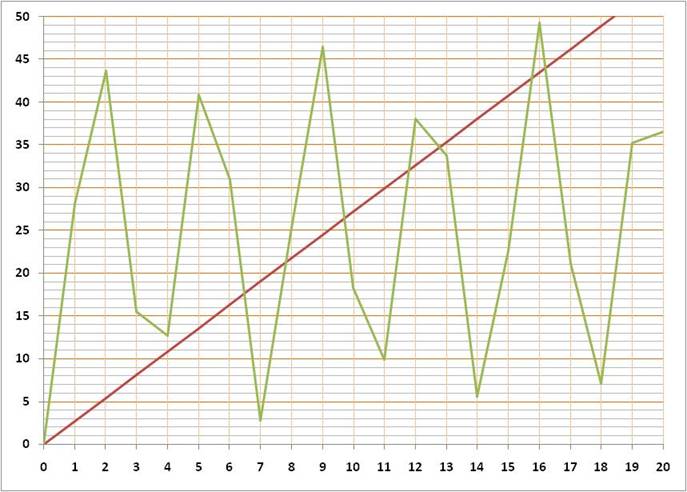
. Pi écart x 100 0 0,00 0,00 1 3,14 14,16 2 6,28 28,32 3 9,42 42,48 4 12,57 43,36 5 15,71 29,20 6 18,85 15,04 7 21,99 0,885 8 25,13 13,27 9 28,27 27,43 10 31,42 41,59 11 34,56 44,25 12 37,70 30,09 13 40,84 15,93 14 43,98 1,770 15 47,12 12,39 16 50,27 26,55 17 53,41 40,71 18 56,55 45,13 19 59,69 30,97 20 62,83 16,81 |
|
|
La courbe marron montre
les multiples de Pi La courbe verte les
écarts absolus à l'entier le plus proche x 100 |
|
|
Mettons en formule Multiple
7 x 3,1415… = 21,99149… Écart
22 – 21,99149… = 0,00885… Écart
x 100 0,885 |
|
|
||
|
C'est l'objet du théorème de Dirichlet, et de ses
applications exposées dans les pages suivantes. |
7 x 3,1415… = 21,99149… 7 x 3,1415… 7 x Pi
Pi
Comment trouver p et q ? |
|
|
|
|
|
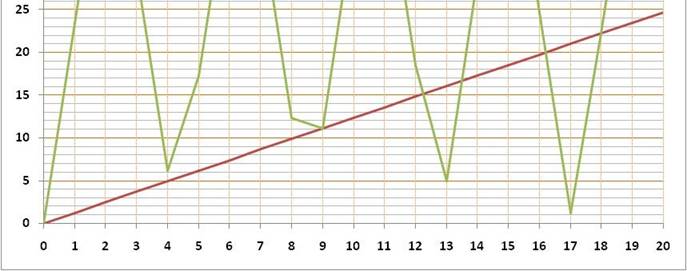
Pour e = 2, 71828 …
la fraction qui se lit sur ce graphique est : 19/7 >>>
En prolongeant la courbe jusqu'à 100, on trouverait 193/71 = 2,7183…
|
|
|
Pour n = 1,23456789 … les fractions qui se lisent sur ce
graphique sont: 5/4,
puis 16/13 et encore mieux 21/17
= 1,235… >>>
En prolongeant la courbe jusqu'à 100, on trouverait 121/98 = 1,2346 … Évidemment, dans ce cas,
plus le numérateur sera proche de 12345… et plus le dénominateur sera proche
d'une puissance de 10 et plus la fraction sera représentative du nombre
initial. |
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()