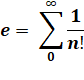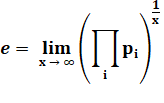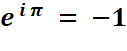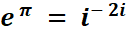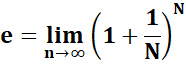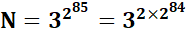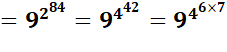|
|||||||||||||||||||||||||||||||||||||||||||
![]()
|
CONSTANTE "e" dite Constante de Neper ou nombre d'Euler
Anglais:
Euler's number, Napier's constant Espagnol: numero de
Euler, constande de Napier Italien: numero
di Eulero, numero di Nepero
Découvert
en 1683 par Jacob Bernoulli
en étudiant les intérêts
composés.
Depuis août 2020, cette constante est connue avec
plus de 31 000 milliards de décimales (David Christie). Proche de 54 jours de calculs ! |
|
APPROCHE |
|
|
Cent premières décimales e = 2,
7182818284 5904523536
0287471352 6624977572
4709369995 9574966967 6277240766
3035354759 4571382178
5251664274 …
Record
Fraction continue e = 2,718 … =
[2 ; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8...] C'est Euler qui calcule la fraction continue de la base des
logarithmes népériens et constate le développement périodique en 1, 2k, 1. Cette périodicité prouve que e est irrationnel. |
|
|
e = 2, 718 281 … |
|
|
e = e1
= exp(1) |
Les logarithmes ont été inventés par Neper;
Il ne connaissait sans doute pas la base
"e". |
|
|
Voir cette
fonction |
|
e = 2,7 1828 1828 459 045 235 36... e = 2,718 281
828 45 90 45 235 36... |
|
|
|
|
|
|
|
|
|
|
|
e = [2 ; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8...] |
Répartition régulière en 2n. |
|
e = 2 + 1 / (1 +
1/ (2 + 2/ (3 + 3/ (4 + 4/ (... e = 1 + 2 / (1 +
1/ (6 + (1/ (10 +... 1/2(2n+1) +... |
|
|
87 / 32 = 2,718 7 878 / 323 = 2,718 2 6 2721 / 1001 = 2,718 281 2 |
|
|
(π 4 + π 5)1/6
= 2,718 281 8086… |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Il est facile d'en
trouver d'autres plus précises. Mais le but est de trouver: Une expression
minimale, ou Une expression
esthétique.
|
|
|
|
|
|
|
|
|
|
|
Fonction exponentielle |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
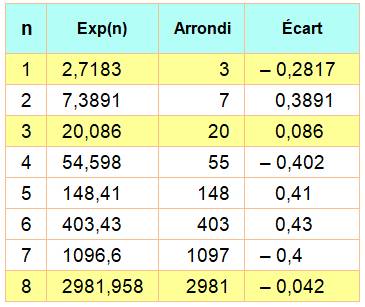
Valeurs
Valeurs avec écart avec un entier
décroissant: 1, 3, 8, 19, 45, 75, 135, 178, 209, 732,
1351, 1907, 5469, 28414, 37373, … OEIS
A079490 Programme de recherche avec Maple
Premières valeurs de
exp(n) avec indication des records( en jaune)
PUISSANCE DE " e "
avec 20 chiffres
Voir Calcul
des puissances de "e" |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||
|
Voici les plus typiques:
La fraction 878 /
323 est souvent choisie; Étant palindromes,
ces deux nombres sont faciles à retenir. Voir
Toutes les réduites de "e" et autres fractions |
|||||||||||||||||||
|
|
||||
|
e = 2,718
281 828 4… Français
Le nombre de lettres de chaque mot donne les chiffres
de "e". Cela dit, la répétition
1828 est également facile à retenir sans autre truc. Anglais
Américain
Attention: "
travel" est au prétérit et, en américain; il s'écrit
"travelled" en anglais. Voir
Mnémotechnique |
||||
|
|
||
|
|
Voir Nombres
presque-entiers en ePi |
|
|
|
||
|
|
|
|
|
|
||
|
|
(démonstration 1995). |
|
|
|
|
|
|
Historique
de
|
||
|
|
|
|
Quelques curiosités de
chiffres
|
|
Voir Exponentielle
d'exponentielle / Puissance de
l'imaginaire
|
|
||
|
En 2004,
Richard Sabey a trouvé cette formule monumentale pour exprimer e avec les
neuf chiffres (pannumérique). Elle
donne 18 457 734 525 360 901 453 873 570 = 1,84 … 1025 décimales |
|
|
|
Explications
avec la valeur de e |
|
|
|
Et avec N
exprimé sous deux formes avec cette propriété des exposants:
3^2p = 9^p, exploitées deux fois. |
|
|
|
En se
souvenant que l'inverse d'une puissance est une puissance négative. |
|
|
Voir Pi en pannumérique
|
|
|||
|
Le quatre plus petits nombres
premiers formés à partir de e 2, 271, 2 718 281, 27182 8182845904 5235360287 4713526624 9775724709
3699959574 9669676277 2407663035 3547594571 DicoNombre: nombre 2, 271,
2
718 281 |
Facteurs pour les dix premiers
nombres formés avec e 2, 2, 2 7, 27, 33 1, 271, 271 8, 2718, 2 x 32 x 151 2, 27182, 2 x 13591 8, 271828, 22 x 67957 1, 2718281, 2718281 8, 27182818, 2 x 13 x 1045493 2, 271828182, 2 x 3 x 45304697 8, 2718281828, 22 x 97 x 179 x 39139 |
||
|
Programme Maple
|
Commentaires Initialisation. Quantité de chiffres demandée en
p. Digits permet de travailler avec une
précision de p chiffres. Calcul d'un nombre e avec p chiffres sans la
virgule. Convert rational forme un nombre
entier sans virgule. Conversion (convert)
pour disposer des chiffres dans une liste et inversion (seq) de
la liste. Analyse des nombres avec de plus en plus de
chiffres de e dans c. Les chiffres successifs sont les i tirés de N. Si le nombre c est premier, l'imprimer. En bleu, résultat du traitement. |
||
Voir Programmation – Index / Brève
427
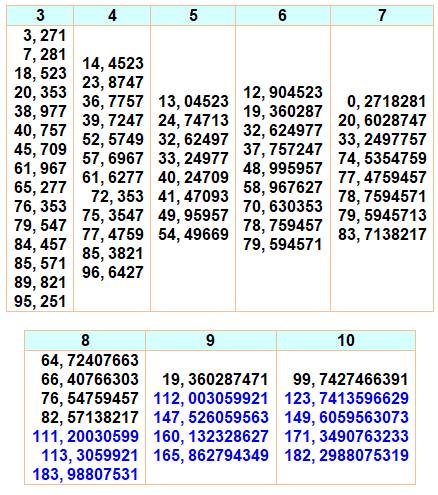
Nombres premiers formés
avec k décimales de e
Exemple: k = 3 donne
271 avec 1 la troisième décimale
k = 4 avec 4523 avec 3 la quatorzième décimale
![]()
|
Suite |
|
|
|
Voir |
|
|
|
DicoNombre |
||
|
Sites |
|
|
|
Cette page |
||
![]()