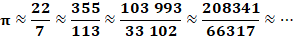|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Conjecture de Duffin-Schaeffer Résolue en 2019 Conjecture à propos de
l'approximation de nombres réels. Approximation diophantienne: trouver
une fraction aussi proche que possible d'un nombre réel et … aussi simple que
possible. Par exemple
pour Pi on peut prendre
3141/1000 ou 22/7. Avec un dénominateur plus petit, la seconde est plus
précise, mais plus difficile à établir. Question:
si on se fixe une approximation au millionième, par exemple, quelle est la
fraction la plus petite approximant un nombre réel comme Pi. Réponse:
selon les choix, on pourra approximer pratiquement tous les nombres ou, au
contraire, aucun. There’s a simple criterion
for whether you can approximate virtually every
number or virtually no numbers,”
said James Maynard of the University of Oxford, co-author of the proof with
Dimitris Koukoulopoulos of the University of Montreal. |
Voir Actualités 2019
|
|
||
|
Nombres iirationnels Les nombres
entiers et les fractions (nombres rationnels) sont bien connus et plutôt rares parmi les
nombres réels. La plus grande
majorité des nombres sont irrationnels,
ces nombres avec une infinité de décimales qui ne peuvent pas être écrits
sous la forme d'une fraction. |
Comment
approcher la valeur de Pi
avec des fractions ?
On ne peut donc jamais atteindre la valeur exacte d'un nombre
irrationnel avec une fraction. Mais comment s'en approcher le plus possible ? |
|
|
Marge d'erreur Le théorème de Dirichlet dit qu'il existe une infinité
de telles fractions d'approximations et le carré de l'inverse du dénominateur
est un majorant du défaut d'approximation. |
|
|
|
Les fractions Plus
généralement, on cherche les approximations des nombres rationnels avec des
dénominateurs appartenant à un ensemble donné de nombres, comme les nombres pairs, ou les nombres premiers. La
question: est-il encore possible, dans ces conditions, de créer une infinité
de fractions se rapprochant d'un irrationnel ? Duffin et
Schaeffer se sont posé cette question:
La
question devient: avec ces paramètres, est-il possible d'obtenir une infinité
de fractions qui approximent tous les nombres irrationnels ? La conjecture
propose une fonction qui détermine si c'est possible ou non. |
Si les dénominateurs appartiennent à l'ensemble {1, 2, 3, 4, 5} on
aura les fractions:
Soit 15 fractions inférieures à 1 dont 4 sont redondantes, car
simplifiées, elles existent déjà ailleurs. Note: l'exemple montre un des problèmes de dénombrement: s'il est facile de
compter toutes les fractions, il est plus difficile d'éliminer les fractions
redondantes. Dans ce cas simple, on peut s'en sortir en utilisant l'indicatrice
d'Euler. |
|
|
|
|||
|
Deux problèmes à résoudre |
1) la redondance des fractions 2) la tolérance admise et le taux de recouvrement qui en résulte |
||
|
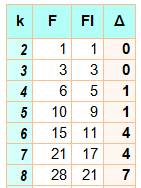
Redondance Ce tableau montre la différence (delta) entre la quantité
de fractions pures (F) et celle des fractions irréductibles (FI) en fonction
du plus grand dénominateur utilisé (k). Pour k = 6, on retrouve nos 15 fractions dont
seulement 11 sont irréductibles. Aleksandr Khinchin avait formulé un théorème
semblable à la conjecture Duffin-Schaeffer mais en comptant toutes les fractions. Éliminer les fractions redondantes n'est pas une mince
affaire. James Maynard et Dimitris Koukoulopoulos ont
trouvé une solution en recourant aux graphes et à la théorie
des graphes. |
Le cas des dénominateurs en nombres entiers est simple (indicatrice
d'Euler). Dans le cas général, la solution a consisté à dessiner le graphe
des dénominateurs: sont reliés ceux qui ne sont pas premiers entre eux (qui ont des facteurs
communs). |
||
|
Tolérance et recouvrement On se
donne donc un jeu de fractions (exemple ½) et une tolérance (0,3), on cherche
à savoir qu'elle est la couverture des nombres réels sur la droite des
nombres.
Avec notre exemple, on note que les fractions retenues sont disposées
de manière irrégulières et, en conséquence, notre fourchette de tolérance
englobe une grand partie de la droite, mais pas toute et parfois en double. |
|||
|
Quantité d'irrationnels dans nos
filets Les
mathématiciens qualifient la couverture (verte) de la ligne des nombres: un e
sommation infinie. Si la
somme tend vers l'infini, l'affaire set gagnée: pratiquement tous les irrationnels
sont approximés. Si la
somme stagne, pratiquement aucuns rationnels ne sont approximés. |
La conjecture offre la
flexibilité de spécifier la tolérance pour chaque dénominateur. Quel que soit la tolérance choisie, l'intervalle contiendra toujours une
quantité infinie de nombres irrationnels. La quantité de nombres embrassée dans
un intervalle, à défaut d'un nombre, est qualifiée par une mesure. |
||
![]()
|
|
||
|
La
conjecture date de 1941. Elle restait une des importantes conjectures non
résolues en théorie métrique des nombres (metric number theory). Une conjecture
analogue avait été résolue en 1990 par Vaughan and Pollington. On
s'approchait de la résolution. Nombreuses
recherche et solutions partielle jusqu'à la résolution obtenue en 2019. Richard James Duffin (1909-1996), physicien
américain. Albert Charles Schaeffer (1907-1957),
mathématicien américain. Voir Contemporains |
Formulation de la conjecture Soit an une suite de nombre positifs distincts et f(n) une
fonction non-négative d'une variable entière.
Avec Phi(n) la fonction totient
d'Euler, si cette expression diverge:
Alors, il a une infinité de solutions à:
pour presque tout
En gros Recherche d'un critère pour
approximer les nombres en excluant certains dénominateurs. |
|
Formulation
en en anglais
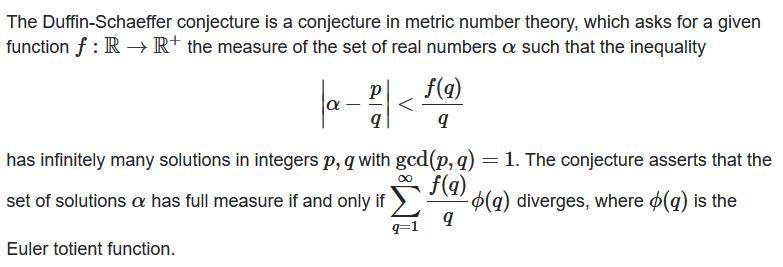
|
|
||
|
Ils ont montré qu'en excluant certains
dénominateurs (même très peu), certains nombres ne peuvent pas être
approximés. Il existe une frontière très fine entre deux
mondes:
|
Dimitris Koukoulopoulos (mathématicien grec, professeur à l'université
de Montréal, à gauche) et James Maynard (Oxford). |
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Sites |
|
|
Cette page |
![]()