Arbres, introduction

Il existe de nombreux types de graphes en forme d'arbres. Graphe qui ressemble aux ramifications d'un arbre. Certains peuvent être dénombrés en utilisant les nombres de Catalan ou d'autres avec la formule de Cayley.

Un arbre (tree) est graphe (graph) connecté dont chaque paire de sommets (vertices) est réunie par un seul chemin appelé arête (edge or branche). Un arbre est un graphe acyclique, sans boucle (cycle). Les sommets sont aussi appelés nœuds (node). Les sommets d'extrémités sont parfois appelés feuilles (leaves).

Un arbre qui possède n sommets aura n–1 arêtes. Ajoutez une arête et vous créez une boucle, un cycle. Le degré (degree) d'un sommet est la quantité d'arêtes auquel il est connecté.

Un arbre est un couple (S, A) avec S la quantité de sommets et A est la quantité d'arêtes.

Un ensemble d'arbres est appelé une forêt (forest).

C'est Arthur Cayley qui, en 1857, introduisit le mot d'arbre pour ces types de graphes.

Sommaire de cette page

>>> Définition

>>> Arbres simples

>>> Arbres multiples

>>> Arbres enracinés

>>> Arbres binaires

>>> Arbres couvrants

>>> Arbres étiquetés

>>> Arbres de Cayley

>>> Arbres de Steiner

>>> English corner

Débutants

Dénombrement

Glossaire

Combinatoire

Anglais: trees (graph theory)

Définitions

ARBRE

Un arbre est un graphe non-orienté, acyclique et connexe tel que le nombre de nœuds (sommets) excède le nombre d’arêtes d’une unité. S = A + 1.

Plus simplement

Un graphe est un arbre si et seulement si entre chaque paire de sommets distincts il existe un chemin unique.

A graph is a tree if and only if between every pair of distinct vertices of there is a unique path.

Arbre (comme graphe) CONNEXE

Il existe une suite d'arêtes permettant d'atteindre deux nœuds (sommets) quelconques de l'arbre.

Arbre (comme graphe) COMPLET

Unique arbre possédant n nœuds (sommets) tous reliés deux à deux par une arête.

Arbre (comme graphe) NON-ORIENTÉ

Arbre dont l'ordre des sommets adjacents n'a pas d'importance.

Arbre (comme graphe) ACYCLIQUE

Arbre qui ne comporte aucune boucle.

Arbres simples – Simple tree

haut

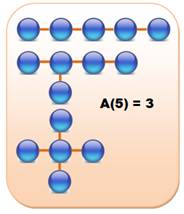
Un arbre simple ou arbre non-étiqueté n'est ni numéroté, ni orienté. Il est composé de sommets et de branches qui se ramifient et se terminent par des sommets à branche unique.

Ils sont trois pour n = 5.

Voir développements Arbres simples

Arbres multiples

haut

Arbre dont un sommet peut être relié à plusieurs sommets.

Simplement nommés: arbres.

Arbres enracinés – Rooted trees

haut

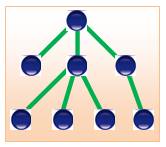
Arbre dont un des sommets est défini comme racine.
D'un sommet, il existe un seul chemin pour remonter à la racine. Passant d'un sommet à l'autre, on passe d'un enfant à son parent (child and parent).

Note: la racine est présentée soit en haut (souvent) soit en bas.

La table des matières d'un livre peut être représentée par un arbre enraciné.

Chaque sommet à des descendants (children).

Note: la présentation du haut est préférable; celle du bas est ambigüe.

Le sommet de gauche représente, par exemple, le livre. Les quatre suivants (rouges), les chapitres. Puis les autres sommets, les paragraphes dans chacun des chapitres.

Arbre enraciné

Arbre type table des matières

Arbres binaires – Binary trees		haut
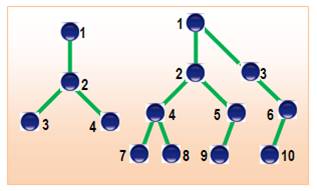
Arbre enraciné dont chaque sommet (parent) n'a que deux successeurs (enfants). Très utilisés en informatique, leurs sommets sont généralement numérotés de gauche à droite et de haut en bas. Binary Tree is defined as a tree data structure where each node has at most 2 children. Since each element in a binary tree can have only 2 children, we typically name them the left and right child.
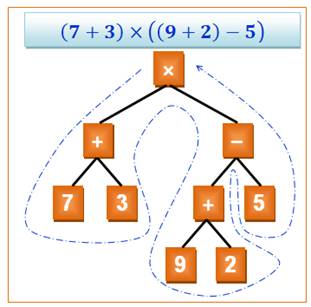
Arbre expression – Expression tree Arbre représentant une expression mathématique (arithmétique ou algébrique). Le pointillé bleu indique le sens de la lecture des nombres et opérateurs.

Arbres couvrants – Spanning trees		haut
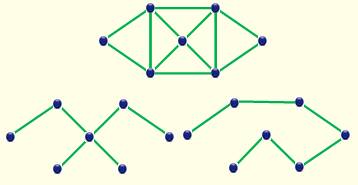
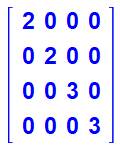
Arbre acyclique (sans boucle) et connecté (d'une seule pièce) dont tous les nœuds sont connectés par un minimum d'arêtes. Un arbre couvrant est un sous-graphe d'un graphe G complet contenant tous les sommets du graphe G. Tout graphe connecté contient un ou plus arbre couvrant. Exemple Le graphe de base (en haut) est incomplet (les sommets 1 et 2 ne sont pas reliés entre eux). Ave ce graphe, il existe huit arbres couvrants. Quantité La quantité d'arbres couvrants est calculée à partir de la matrice des degrés (quantité d'arêtes par nœud), et en utilisant l'algorithme de Kichhoff. Matrice des nœuds	Graphe complet et deux de ses arbres couvrants Arbre couvrant incomplet pour quatre sommets
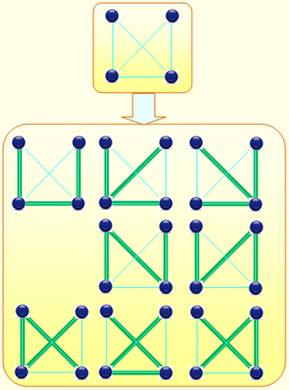
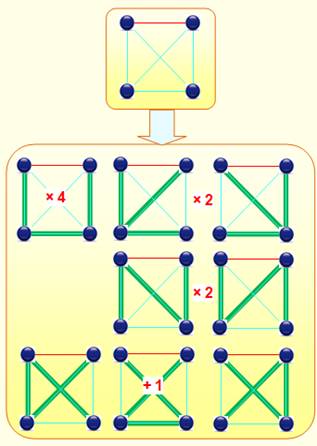
Quantité d'arbres couvrants complets Dans le cas des arbres couvrants complets (avec toutes les liaisons possibles entre sommets), la quantité est donnée par la formule de Cayley. Q = n^n–2 Q = {1, 1, 3, 16, 125, 1296, 16807, 262144, 4782969, 100000000, …} Soit 125 arbres couvrants complets pour n = 5. Illustration avec n = 4 On reprend l'exemple précédent en complétant le graphe par le trait horizontal rouge. L'indication chiffrée en rouge identique les arbres supplémentaires du fait du passage permis en haut. Le U peut alors prendre quatre positions. On a bien: 4 + 2×2+ 2×2 + 3 + 1 = 16.	Arbre couvrant COMPLET pour quatre sommets

Arbres étiquetés – Labeled trees

haut

Exemple

Avec les arbres numérotés à trois nœuds, les numéros des extrémités sont interchangeables.

Seul le numéro central est original. Soit trois possibilités (1, 2 ou 3).

Il existe seulement trois arbres étiquetés d'ordre 3. Les trois autres, en inversant les extrémités, sont redondants.

Voir développements Arbres étiquetés

Formule de Cayley

Arbres de Cayley – Cayley trees		haut
Arbres Cayley d'ordre n Arbres dont les nœuds internes sont tous de degré n (même quantité d'arêtes). Note: les arbres étiquetés sont parfois nommés arbres de Cayley car leur quantité est exprimée par la formule de Cayley. Pour l'ordre 3 Ils sont aussi appelés arbres trivalents, ou arbres borons. Il y en a 1 seul a 4 sommets; 0 à 5 sommets, 1 à 6 sommets; etc. Liste à partir de n = 1 pour l'ordre 3 1, 1, 0, 1, 0, 1, 0, 1, 0, 2, 0, 2, 0, 4, 0, 6, 0, 11, 0, 18, 0, 37, 0, 66, 0, 135, 0, 265, 0, 552, 0, 1132, 0, 2410, 0, 5098, 0, 11020, 0, 23846, … OEIS A052120	Exemples d'arbres de Cayley d'ordre 3 Un seul arbre trivalent pour 4, 6 ou 8 sommets Exemples d'arbres de Cayley d'ordre 4
Arbre de Cayley Avec trois sommets et sept niveaux. Chaque niveau compte: 1, 3, 6, 12, 24, 48 et 96 sommets; donc, 96 feuilles.

Arbres de Steiner – Steiner trees

haut

Arbres de Steiner

Arbres entre n points initiaux et k points intermédiaires dits points de Steiner.

Avec ces points, il est possible de concevoir un réseau reliant tous les points dont la longueur totale est minimale.

Pour quatre points initiaux (longueur du réseau: 3), et deux points intermédiaires, il est possible de ramener la longueur du réseau à 2,73…

Dans tous les cas, les points de Steiner sont entourés de trois angles de 120°.

Développements en Arbres de Steiner

English corner

A tree is a connected graph containing no cycles.

A forest is a graph containing no cycles. Note that this means that a connected forest is a tree.

A graph T is a tree if and only if between every pair of distinct vertices of T there is a unique path.

A graph is a tree if and only if between every pair of distinct vertices of there is a unique path.

Let T be a tree with v vertices and e edges. Then e = v – 1

Voir Anglais pour le bac et pour les affaires

Haut de page

Retour	Arbre – Index Graphe – Introduction Graphe planaire
Suite	Arbres à dénombrement avec nombres de Catalan Arbres de distribution Chemin le plus court Vocabulaire des graphes	Coloration des graphes (nombre chromatique) Graphes et problèmes NP Petit monde Sept amis autour d'une table
Voir	Code Gray Croissance logistique Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index	Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ Trois maisons (énigme des -)
Sites	Arbre (théorie des graphes) – Wikipédia Trees – Lecture 1 – notes 2016 Binary Tree Data Structure – Geeksforgeeks – Description et programmation en C++ Formule de Cayley – Wikipédia OEIS A000272 – Number of trees on n labeled nodes: n^(n-2) with a(0)=1 Cayley Tree – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/ArbreG.htm