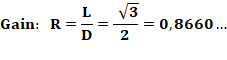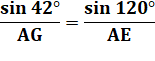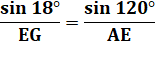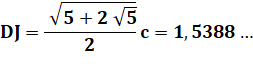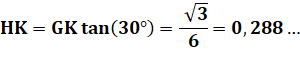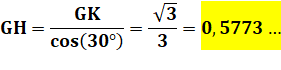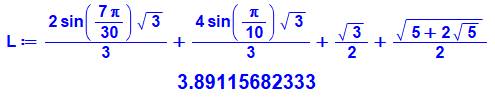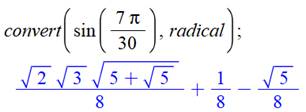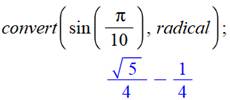|
Édition du: 08/03/2024 |
|
INDEX |
GRAPHES |
||
Faites
un double-clic pour un retour en haut de
page
![]()
|
Minimiser la voirie (le réseau) Arbres de Steiner Étant donné n villes (ou maisons), il s'agit de trouver le réseau de
voirie qui comptera le minimum de kilomètres. Toutes les villes doivent être
desservies même si le chemin doit passer par d'autres villes intermédiaires. Deux types de solutions:
Les solutions avec croisements sont les plus performantes. S'il est
facile de trouver les solutions pour trois, quatre ou cinq villes, le
problème devient vite incroyablement difficile à résoudre (NP-Complet).
Problème d'optimisation d'un réseau selon le facteur coût. |
||
|
|
Sommaire de cette page >>> Trois villes –
Arbre couvrant et arbre de Steiner >>>
Quatre villes – Diverses possibilités >>>
Points de Steiner >>>
Voirie minimale pour cinq villes >>>
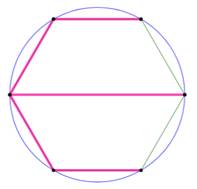
Arbre de Steiner d'ordre 6 >>>
English Corner |
Débutants Glossaire |
Anglais: Connect the
towns, the motorway problem (Isenberg
1975)
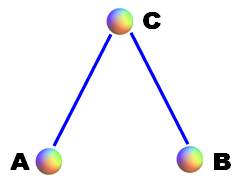
Arbre couvrant (spanning tree) D'une manière générale, un arbre couvrant d'un
graphe est un arbre inclus dans le graphe qui connecte tous les sommets du
graphe. Avec trois sommets, un arbre couvrant nécessite
deux arêtes (ici AC et CB). C'est l'arbre couvrant qui minimise la longueur
totale du graphe (L = 2). |
|
|
|
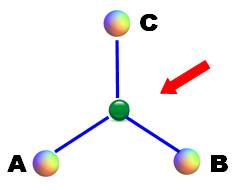
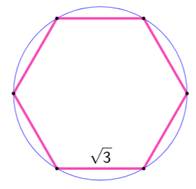
Arbre de Steiner (Steiner tree) Il est possible de réduire la longueur totale de
l'arbre en ajoutant des points intermédiaires. Avec trois sommets, un point central (vert)
réduit la longueur du totale du réseau. Avec un triangle
équilatéral, le point optimum se trouve au centre du triangle et S = √3. |
|
|
|
Gain de longueur Le gain de longueur entre un arbre de Steiner et
un arbre couvrant d'ordre 3 est : |
|
|
|
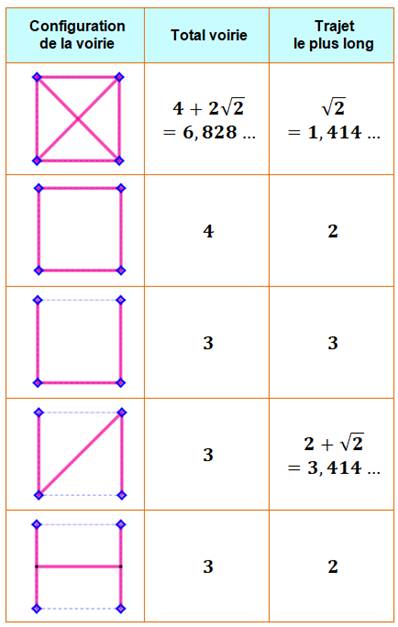
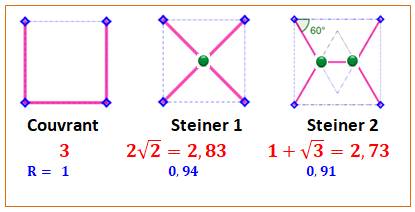
Relier quatre villes Les quatre villes sont situées aux sommets d'un carré. Elles
doivent être accessibles les unes par les autres. Il existe un chemin qui permet de rejoindre une
ville aux trois autres. Deux questions Quelle est la configuration de la voirie qui
minimise le trajet le plus long parmi tous ? Quelle est la configuration qui minimise la
quantité d'asphalte. Autrement-dit: quelle est la configuration dont la
longueur totale de la voire est la plus courte ? Piste Toutes les villes sont reliées par une route
(configuration du haut):
Les essais suivants réduisent ces valeurs jusqu'à
aboutir aux minimums possibles. Solutions (en
jaune) Les routes limitées aux diagonales offre le plus
petit trajet le plus long avec 1, 41 km pour chacun. Pour la voirie minimum, la solution passe par des
routes posées sur deux triangles équilatéraux opposés. La longueur totale des
routes est alors:
2,73 km Il a fallut poser deux points de croisement
intermédiaires. |
|
|
Voir Explications
et calculs / Énigme du
raccordement des cinq maisons
Arbre couvrant (spanning tree) D'une manière générale, un arbre couvrant d'un
graphe est un arbre inclus dans le graphe qui connecte tous les sommets du
graphe. Avec trois sommets, un arbre couvrant nécessite
deux arêtes (ici AC et CB). C'est l'arbre couvrant qui minimise la longueur
totale du graphe (D = 2). |
|
|
|
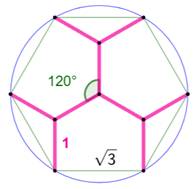
Arbre de Steiner (Steiner tree) Il est possible de réduire la longueur totale de
l'arbre en ajoutant des points intermédiaires. Avec trois sommets un point central (vert) réduit
la longueur du totale du réseau. Avec un triangle équilatéral, le point optimum,
dit point de Steiner, se trouve au centre
du triangle et L = √3. Notez que les angles
autour du point de Steiner valent 120°. |
|
|
|
Avec quatre sommets L'arbre couvrant les quatre points, sommets d'un
carré, compte trois arêtes au minimum (D = 3). Il est possible de réduire la longueur totale du
réseau en introduisant un ou deux points intermédiaires. La longueur est alors diminuée de 6% pour un
point et de 9% pour deux points. Ajouter d'autres points ne réduit pas la
longueur. Notez que les angles
autour du point de Steiner valent tous 120°. |
|
|
|
Propriétés Tous les points de Steiner sont entourés de trois
angles de 120° (prouvé). Un arbre de Steiner minimal possède au plus n – 2
points de Steiner. |
Rapport de longueurs entre un arbre de Steiner minimal et un arbre
couvrant minimum: On a longtemps pensé qu'il ne pouvait pas être
inférieur à √3 / 2 = 0,866… Valeur trouvée en 1978:
|
|
|
Voirie minimale pour cinq villes Arbre de Steiner d'ordre 5 |
|||||||
|
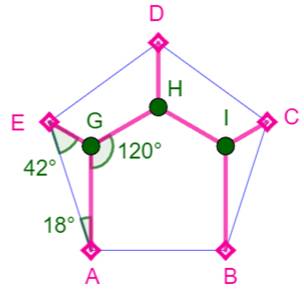
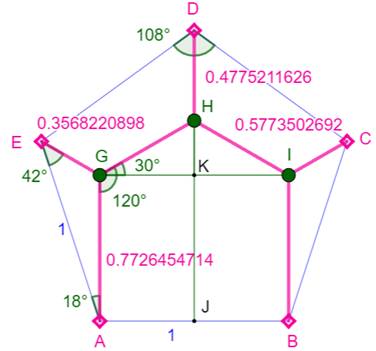
Pour cinq villes ou cinq points L'arbre de Steiner minimum pour cinq points disposés
aux sommets d'un pentagone
régulier est montré sur cette figure. Pour sa construction (en suivant la
figure):
|
|
||||||
|
Angles de l'arbre de Steiner 5 Comme tous ces arbres, les points de Steiner sont
entourés d'angles de 120°. L'angle interne
du pentagone vaut 108°. Dans le triangle AGE, l'angle en A vaut: 108 – 90
= 18°. Le troisième angle de ce triangle vaut: 180 – 120
– 18 = 42°. Dimensions de l'arbre de Steiner 5 Toujours dans le triangle AGE, avec la loi
des sinus:
Hauteur
du pentagone:
Hauteur du triangle isocèle GHI: |
Dimensions du réseau d'ordre 5 Ce réseau comporte trois
points de Steiner: G, H et I.
Longueur totale du réseau L = 2(0,772… + 0,365… + 0,577…) L = 3,891… |
||||||
|
Côté du triangle isocèle GHI: Arête DH: Longueur du réseau pour pentagone
régulier unité
Valeur calculée
avec Maple et vérifiée avec GeoGebra Pour information Valeur des sinus
avec
radicaux
|
|||||||
|
Deux arbres couvrants et l'arbre
de Steiner minimal. Quatre points intermédiaires.
Il est unique. |
|||
|
|
|
|
|
|
L = 6√3 Trajet le plus long: 3 |
L = 6√3 Trajet le plus long: 2 |
L = 6 Trajet le plus long: 4 |
|
Une des topologies pour arbre de Steiner d'ordre 7
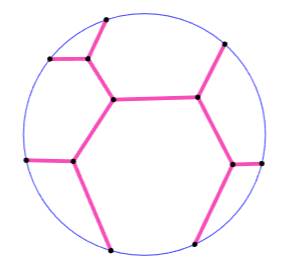
Mais l'heptagone n'est pas régulier
|
The motorway
problem is an interesting one in optimisation. Suppose that
there are four cities, A, B, C, and D, located at the four corners
of a square with sides of length 1. A network of motorways is
to connect all four cities in the shortest distance possible in order to
optimise construction costs. What
configuration of motorways will yield the minimum total distance ? Suppose a
finite set of points are randomly scattered about in the plane. How can they
be joined by a network of straight lines with the shortest possible total
length? It is easy
to see that the shortest network must be a tree, that is a connected network
containing no cycle. If no new
points can be added to the original set of points, the shortest network
connecting them is called a minimum spanning tree. |
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()