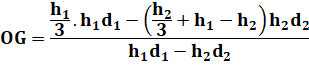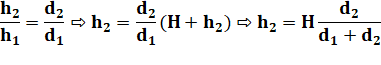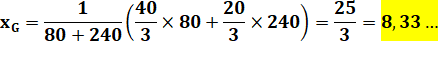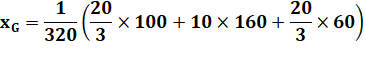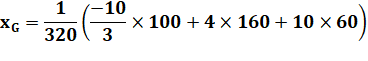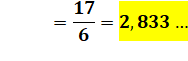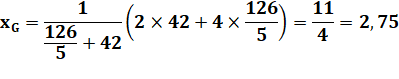|
||||||||||||||||||||||||||||||
![]()
|
Centre de gravité du TRAPÈZE Tout d'abord, établissement
de la formule donnant la position du centre de gravité du trapèze isocèle. Ensuite, une solution
graphique pour le trapèze quelconque. Nous
confirmerons en décrivant deux manières de calculer analytiquement la
position de ce centre de gravité. |
|
|
||
|
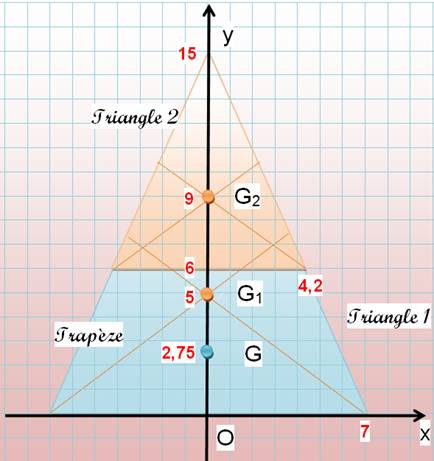
Le trapèze isocèle est
en fait un triangle
isocèle (T1) étêté d'un triangle isocèle (T2). Le centre de gravité de
chacun des triangles isocèles se trouvent sur l'axe de symétrie au 1/3 de
distance de la base (point de concours des médianes).
Avec
Thalès, calculons la longueur de la demi-base d2 du triangle T2:
Chacun de
ces centres supportent la "masse" du triangle:
|
|
|
|
Le centre de gravité du
trapèze est tel qu'il égalise la différence des moments
(différence car retrait du triangle T2). |
67,2
OG = 105 x 5 – 37,8 x 9 = 525 – 340,2 = 184,8 OG = 184,8 / 67,2 = 2,75 |
|
|
Calcul formel Notez que la position du
centre de gravité ne fait intervenir que les deux hauteurs. La taille de la base
n'influe pas. Normal, si le trapèze est plus évasé, il n'en comporte pas
moins autant de matière de chaque côté. |
|
|
|
Le trapèze étant le plus
souvent défini par sa hauteur H et ses bases d1 et d2,
la position du centre de gravité devient Formule valable que d1 et d2
représentent la longueur des bases ou la demi-longueur (la proportion ne
change pas). |
|
|
|
|
||
|
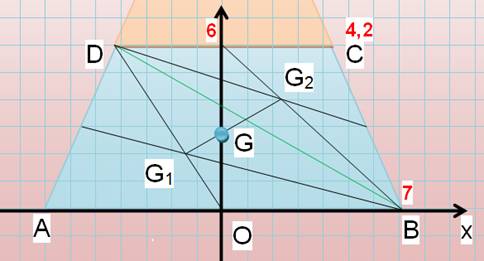
Découpez le trapèze en deux triangles. Dessinez leur centre de gravité G1 et G2. Nous sommes dans le cas de deux
points: G se trouve sur le segment G1G2. Par ailleurs, la médiane M1M2
partage le trapèze en deux trapèzes de même aire. Même
quantité de matière de part et d'autre. G se trouve quelque part sur cette
médiane du trapèze. Le centre de gravité est à l'intersection de ces deux
droites (bleues). |
|
|
|
|
||||
|
|
||||
|
Triangle bleu |
C (8, 20) D (14, 0) |
A1 = ½ 20 x
8 = 80 |
xG1 = 1/3
(0+8+14)=22/3 = 7,33… yG1 = 1/3
(20+20+0)=40/3 = 13,33… |
|
|
Triangle vert |
B (0, 20) D (14, 0) |
A2 = ½ 20 x
24 = 240 |
xG2 = 1/3
(-10+0+14)=4/3 =1,33… yG2 = 1/3
(0+20+0)=20/3 = 6,66… |
|
|
Barycentre |
G1 (22/3,
40/3) G2 (4/3,
20/3) |
|
||
|
|
||||
|
|
||||
|
Triangle bleu gauche |
B
( 0, 20) O
( 0, 0) |
A1
= ½ 20 x 10 = 100 |
xG1
= 1/3 (-10+0+0)=-10/3 = -3,33… yG1
= 1/3 (0+20+0)=20/3 = 6,66… |
|
|
Rectangle vert |
|
A2
= 8 x 20 = 160 |
xG2
= 4 yG2
= 10 |
|
|
Triangle vert droit |
C
( 8, 20) D
(14, 0) E
( 8,
0) |
A3
= ½ 6 x 20 = 60 |
xG3
= 1/3 (8+14+8)=30/3 =10 yG3
= 1/3 (20+0+0)=20/3 = 6,66… |
|
|
Barycentre |
G1
(-10/3, 20/3) G2
(4, 10) G3
(10, 20/3) |
|
||
|
|
||
|
Aire T1 = 6 x 7 = 42 A (
-7, 0) B (
7, 0) D (-21/5 , 6) G1 (-21/15, 2) Aire T2 = 6 x 21/5 = 126/5 B (
7, 0) D (-21/5 , 6) C ( 21/5 , 6) G2 (7/3, 4) |
Note: 21/5 = 4, 2 |
|
|
Centre de gravité |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/STATIQUE/Trapeze.htm |