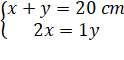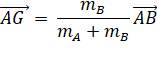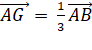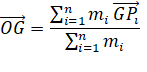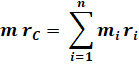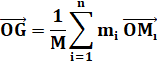|
|
Définition |
|
Voir vocabulaire:
Centre de gravité / centre de masse / centre d'inertie /
centre géométrique …
|
Approche |
-
Évidemment, si les masses
sont différentes, le point d'équilibre n'est plus au milieu! -
Supposons une masse double à
gauche par rapport à celle de droite. -
Il faudra déplacer le
couteau (symbolisé ici par un triangle équilatéral)
vers la masse la plus importante, donc vers la gauche. -
Le fléau sera plus court à
gauche qu'à droite dans le rapport des masses (voir le calcul ci-contre).
|
Barre simple
Barre avec masses
Calcul
Alors 3 x = 20 et x = 6,66… et y = 13,33… |
![]()
|
On construit le parallélogramme CGBA" de
manière à faire apparaître la somme des vecteurs
GB et GC (relation de Chasles):
Or cette somme est
connue (voir définition ci-dessus):
En comparant les deux
égalités:
Isobarycentre et centre de gravité d'un triangle
homogène sont confondus C'est le point de concours des médianes. Voir Calcul
du centre de gravité du triangle |
![]()
|
Barycentre |
Barycentre: point
d'application de la résultante des actions de la pesanteur sur toutes les parties
d'un corps; c'est le centre de gravité
de ce corps. Barycentre de trois points A de
masse mA, B de masse mB et C de masse mC. Le
barycentre est l'unique point vérifiant:
Même
définition que pour l'isobarycentre, à ceci près que les vecteurs sont
pondérés par un coefficient mI; évidemment cette formule peut-être
généralisée à une quantité de points quelconque. L'isobarycentre
est un barycentre dont tous les coefficients de pondération valent l'unité
(masse homogène pour reprendre l'analogie avec le centre de gravité). Barycentre de n points Soit n points P1, P2
… Pn d'un espace affine
|
![]()
|
|
On peut prendre les points dans
l'ordre que l'on veut sans changer le barycentre.
Deux points peuvent être
remplacés par leur barycentre affecté de la somme des deux coefficients
(masses). Il est possible de trouver le barycentre d'un système de points de
proche en proche en remplaçant des couples de points par leur barycentre.
La relation de Chasles permet de
calculer:
Application numérique au cas du
haut de la page. mA = 2 et mB
= 1;
-
Centre de gravité: A, 1; B, 1; C, 1 -
Centre du cercle
inscrit: A, a; B, b; C, c -
Centre du cercle exinscrit
en A: A, -a; B, b; C, c -
Centre du cercle
circonscrit: -
Orthocentre: |
![]()
|
Anglais En savoir plus |
Centre of gravity: when
a system of particles or a rigid body with a total mass m experiences a
uniform gravitational force, the total effect on the system or body as a whole
is equivalent to a single force acting at the center of gravity. This point
coincides with the center of mass. Center of mass (or
centroid): Suppose that particles P1,
P2 … Pn, with corresponding mass m1, m2 … mn (total mass m), have position
vectors r1, r2 … rn, respectively. The
center of mass (or centroid) is the point with position vector rC
given by:
|
![]()
![]()
Centre de gravité /
centre de masse / centre d'inertie / centre géométrique …
|
Centre de … |
Beaucoup de
termes pour des choses quasi-semblables dans un monde homogène, docile …
Nous allons
tenter de décrire les nuances. |
|
Barycentre Barycenter |
Centre d'un système composé d'objets massiques tel que tout le système
est résumé en ce point. C'est la position moyenne de
tous les points du système pondérée par la masse de chaque point. En géométrie
comme en physique, c'est une généralisation de la notion de masse à n'importe
quelle valeur numérique exprimant une grandeur ou non (ex: charges électriques,
quantité de votants dans les villes …) Le calcul
consiste à trouver le point qui annule une somme pondérée de vecteurs. Le barycentre
trouve son intérêt du fait du principe
d'équivalence qui permet:
|
|
Centre géométrique Isobarycentre Centroid Geometric center |
Centre géométrique et centre isobarycentre sont totalement synonymes. Le centre
géométrique d'un objet géométrique est la position moyenne (arithmétique) de tous
les points de l'objet. C'est un point
tel que si la figure était une plaque de métal homogène d'épaisseur
constante, alors la matière serait équirépartie autour de ce point. Dans un
champ gravitationnel homogène, l'objet posé sur la pointe d'un crayon en ce point
tiendrait en équilibre. Lorsque la
figure géométrique présente un centre de symétrie,
comme pour le disque ou le carré, le centre géométrique est confondu avec le
centre de symétrie. L'isobarycentre
donne le moyen de visualiser le calcul. Les pondérations sont égales à
l'unité. Position du
centre de gravité:
|
|
Centre de gravité Gravity center |
Ce point
s'appelait autrefois centre de poids. C'est le terme
le plus connu du grand public. Pour un corps homogène, c'est son centre géométrique. Point
d'application du poids, résultante des forces de gravité ou de pesanteur.
Possibilité de simplification: le poids est une force qui s'applique en un
point unique, G du corps. Le centre de gravité dépend du champ de gravitation auquel le corps est soumis. Ce champ est la plupart du temps uniforme dans le corps considéré C'est le point
pour lequel le moment
total des forces de gravité est nul. Définitions Point d'un corps
situé de telle façon qu'une force verticale suffisante, appliquée en ce
point, tiendra le corps en équilibre Point par lequel
passe constamment la résultante des poids des molécules qui composent un
corps quelle que soit la position donnée à ce corps; il y a équilibre toutes
les fois que la verticale du centre de gravité passe par le point d'appui ou
de suspension. (Littré) Point
d'application de la résultante des forces de pesanteur qui s'exercent sur
l'ensemble des particules composant un corps; en géométrie, synonyme de
centre d'inertie. (Larousse) |
Comparaison
|
Il y a entre centre de masse et centre
de gravité le même type de différence qu'il y a entre masse et poids.
Les premiers sont absolus alors que les
seconds dépendent du champ de gravitation.
En pratique, le champ de gravitation est considéré comme homogène et les deux
centres sont confondus. |
|
Centre de masse Centre d'inertie Center of mass Inertia center |
Barycentre des masses. Centre de masse;
point équivalent où serait concentrée toute la masse de l'objet tout en
créant exactement le même effet de gravitation
(le même champ de gravitation). Masse inerte et masse grave
étant identique, le centre d'inertie est confondu avec le centre de masse. Le centre de
masse ne dépend que de l'objet. Le centre de gravité dépend du champ de
gravitation. Sur Terre, il est un
juste un peu plus bas que le centre de masse car la pesanteur est un peu plus
grande sur la partie basse que sur la partie haute. Différence hyperfaible et
négligeable la plupart du temps. Point
d'application des effets d'inertie, c'est-à-dire du vecteur variation de
quantité de mouvement. Si un objet est
en rotation autour d'un axe ne passant pas par ce centre d'inertie, l'objet
ne tourne pas rond. Il y a un balourd. Si le champ de
gravité est uniforme, le centre d'inertie est confondu avec le centre de
gravité |
|
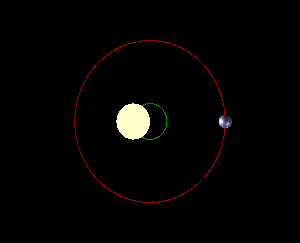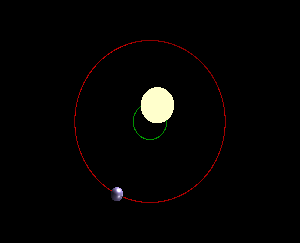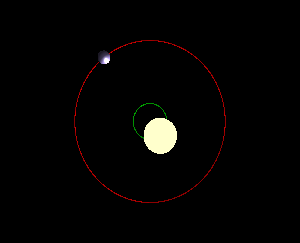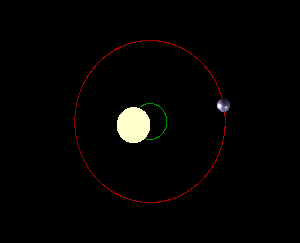
Barycentre entre une étoile et une
grosse planète |
Le centre de
masse (barycentre) de deux objets céleste est situé sur l'axe joignant les
deux centres. Si l'un deux est
une étoile et l'autre, une petite planète, le centre de masse est très proche
du centre du gros objet et même dans le gros objet (cas du couple
Soleil-Terre). Avec le couple Soleil-Jupiter
de point est externe au Soleil. Cette situation
affecte le mouvement des deux objets. En particulier, les deux objets sont en
orbite avec le centre de masse comme centre de l'orbite. Cette
oscillation, plus ou moins importante, du gros objet (étoile) est un témoin
de la présence d'une planète en orbite autour de lui. C'est un mode de
détection des exo-planètes.
|
Source: What is a barycenter –
Nasa
![]()
|
Barycentre Centre de
Gravité Index
|
Général
Méthodes
Objets
Divers
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Vocabula/GlosB/Barycent.htm
|
![]()