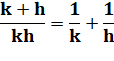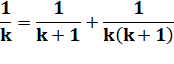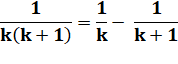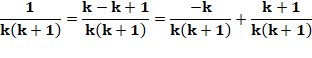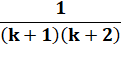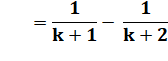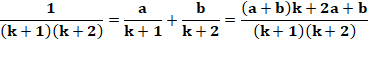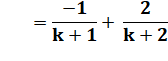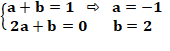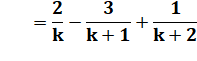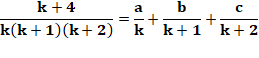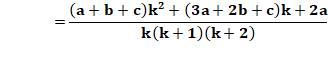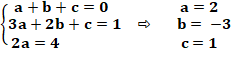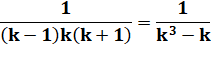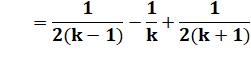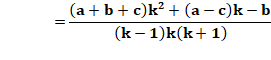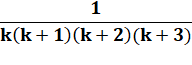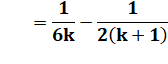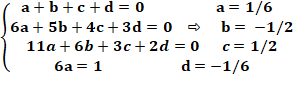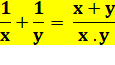|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
RELATIONS |
CALCULS |
|
|
|
/ |
|
|
|
|
|
|
|
Idem ci-dessus ou:
|
|
|
|
|
|
|
|
Même développement
que ci-dessus
|
|
|
|
|
|
|
|
|
|
Même développement
que ci-dessus
|
|
|
|
Voir Application au calcul de somme
de suites / Brève
860
![]()
|
|
|
|
Propriété La somme des inverses est égale au rapport de la somme sur le
produit:
Exemple Avec 1/2 et 1/3 On connaît la somme de deux nombres: x
+ y = 10 Le produit:
x . y = 20 Quelle est la valeur de la somme des
inverses? C'est: 10
/ 20 = 0,5 Cas
particulier important
|
|
|
|
|
|
Bien entendu, pour
cette énigme, nous aimerions connaître la
valeur des deux nombres x et y.
Voir Équations
du deuxième degré - Somme et produit On note que: Les deux couples de solutions sont
symétriques. Les
deux solutions pour x ou pour y sont
symétriques par rapport à 5 = Somme / 2. Solution
générale : équations
somme/produit |
|
|
|
|||||||||||||
|
Exemples:
Toutes les
valeurs réelles pour S et P < 6:
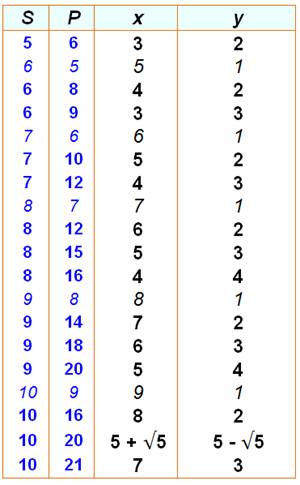
Les
valeurs entières pour S < 10 et P < 21 Avec rappel du puzzle. En italique, cas triviaux pour lesquels y =
1.
|
|||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()