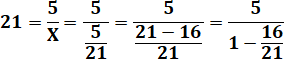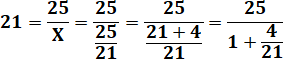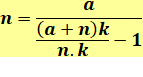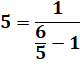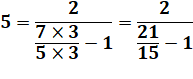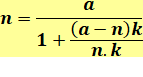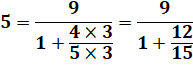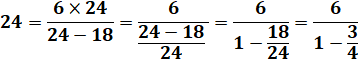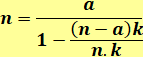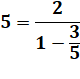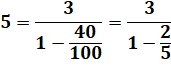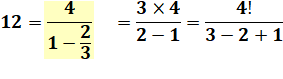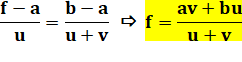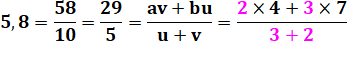|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
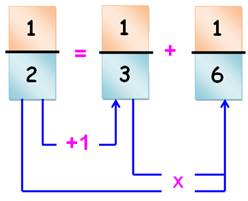
FRACTIONS UNITAIRES et ÉGYPTIENNES Comment les construire. |
|
|
||
|
Connue notamment de Fibonacci.
|
|
|
Suite en Table et comparaison entre fractions usuelles
|
|
||
|
|
|
|
|
|
Exemple
avec a quelconque
Exemple
avec a = entier > à k/2
|
|
|
|
||
|
|
Exemple
Relation
avec les moyennes
|
|
|
|
||
|
|
|
|
|
|
|
|
Voir
exemples et comment faire fonctionner cet algorithme >>> |
|
|
|
|||
|
Comment déguiser un nombre
en fraction ? |
Prenons 21 à "déguiser" à l'aide de 5:
Idem en plus
|
||
|
Forme générique en moins Alors n < a et k quelconque |
Le facteur k n'est là que si on désire un
dénominateur particulier. Alors la fraction est évidemment réductible. |
n = 5, a = 1, k = 1
n = 5, a = 2, k = 3
|
|
|
Forme générique en plus Alors n > a et k quelconque |
Le facteur k n'est là que si on désire un
dénominateur particulier. Alors la fraction est évidemment réductible. |
n = 5, a = 6, k = 1
n = 5, a = 9, k = 3
|
|
|
Plus élaboré … |
Prenons 21 à déguiser à l'aide de 6:
|
||
|
Forme générique en moins Avec a < n |
Le facteur k n'est là que si on désire un
dénominateur particulier. Alors la fraction est évidemment réductible. |
n = 5, a = 2 et k = 1
n = 5, a = 3 et k = 20
|
|
|
Les multiples façons de "déguiser" les
nombres de 3 à 10
Exemple de devinette: Comment écrire 12 avec seulement les nombres 1, 2, 3 et 4 ? Une solution avec ce type de fraction et d'autres solutions comme dans
les jeux classiques
avec les nombres.
|
|||
|
|
||
|
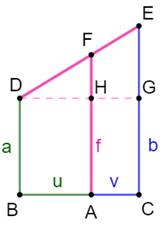
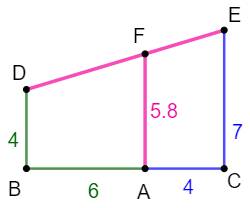
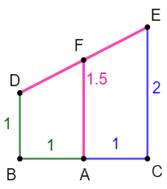
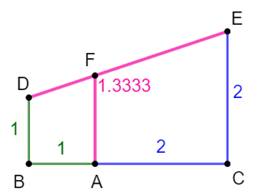
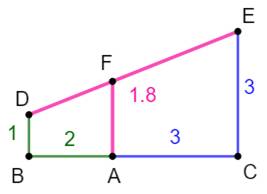
Formulation Dans le
triangle DGE, application du théorème de
Thalès:
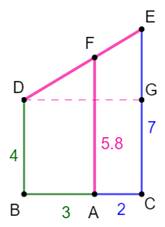
Application On se propose de construire une longueur égale à
5,8. Le dénominateur est choisi pour faire u + v,
sachant que u et v sont les multiplicateurs de deux nombres au numérateur. Notez le produit en
croix au numérateur. Il existe généralement quantité de solutions,
comme: Il y en a 1828 pour (a, b, u et v) de 1 à 100,
et, en général, une infinité. |
|
|
|
Exemples
|
||
Voir Constructions de fractions
simples / Division d'un
segment / Brève
528
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()