NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/12/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Base de la Géométrie
Débutants Angles	ANGLES				Glossaire Géométrie
INDEX Angles Bases Géométrie	Première	Angles	Angles orientés	Exemple de calculs
		Sommaire de cette page >>> Problème >>> Utilisation de l'inversion de vecteurs >>> Addition d'angles (relation de Chasles, simple) >>> Utilisation simple de la relation de Chasles >>> De la géométrie >>> Vecteurs distants >>> Angles proches

Les ANGLES orientés

Exemples expliqués en détails

Voici un exercice souvent donné sous cette forme ou sous une forme voisine pour s'entraîner aux calculs sur les angles orientés.

Les calculs vont être expliqués pas à pas au bénéfice du plus grand nombre.

Problème
Voici la figure objet des questions: un carré ABCD, et un triangle équilatéral BCM en chapeau du carré. Comme nous allons parler d'angles, constatons immédiatement que dans: le carré les angles valent 90° = le triangle équilatéral, ils valent 60° = . En outre, observons que tous les segments de cette figure ont même longueur.

Utilisation de l'inversion de vecteurs
Valeur de l'angle ? Observations Par lecture sur la figure, je constate que la valeur est de 90° = et en traçant le vecteur AA' qui représente le vecteur DA, cet angle est dans les sens horaire donc négatif. Résolution J'utilise les relations d'égalité des angles orientés pour calculer l'angle; ensuite je calcule.
Calcul pas à pas: Le fait d'indiquer que l'angle est connu à k tour près, k valant tout nombre entier, y compris 0, est n'a pas d'autres impératifs que l'extrême rigueur mathématique sans autres effets à ce stade.

Addition d'angles (relation de Chasles, simple)
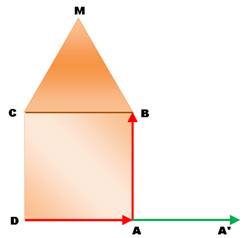
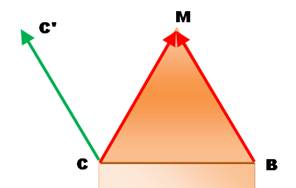
Valeur de l'angle ? Observations Par lecture sur la figure, je constate que la valeur est de 90°+ 60° = et cet angle est dans les sens antihoraire donc positif. L'angle DCM mesure 150°.
Calcul pas à pas:

Utilisation simple de la relation de Chasles
Valeur de l'angle ? Observations Par lecture sur la figure, je constate que la valeur est de 60° = et en traçant le vecteur CC' qui représente le vecteur BM, cet angle est dans les sens antihoraire donc positif. Résolution Nous utilisons d'abord la relation de Chasles puis une des égalités qui retourne un vecteur.
Calcul pas à pas:

De la géométrie!
Valeur de l'angle ? Observations Par lecture sur la figure, je constate que la valeur est inférieure à celle de l'angle BCM, soit inférieure à 60°. je ne dispose d'aucun angle de cette sorte. Nous n'avons que 60° et 90° en magasin. Résolution Nous devons recourir à la géométrie classique
Par construction du carré: Par construction du triangle équilatéral: Conséquence:	DC = CB CB = CM DC = CM
Le triangle DCM est isocèle et ses angles à la base (A) sont égaux. Nous savons également que l'angle au sommet (DCM) vaut 150° =
Bilan	soit 15°

Vecteurs distants
Valeur de l'angle ? Observations Par lecture sur la figure, je constate que la valeur est de (90 + 15) + 90 =195°= et cet angle est dans les sens antihoraire donc positif. Résolution Plein effet de la relation de Chasles. Je pense que je viens de calculer l'angle DCM et je vais l'utiliser.
Calcul pas à pas: Note en ligne 2: Pi + Pi = 2 Pi, soit un tour; nous le faisons entrer dans le 2k Pi dont on sait que la valeur de k est un entier quelconque.

Angles proches
Valeur de l'angle ? Avec I le point d'intersection des diagonales du carré. Observations Par lecture sur la figure, je constate que BM et IC sont presque parallèles mais ne le sont pas. l'angle semble bien petit. Je remarque que IBM = 45°+ 60° = 105° Et aussi que BIC = 90°. Je devine que mon angle vaut 105 – 90 = 15°. Résolution Dan le carré, les diagonales se coupent en leur milieu et à angles droits; les quatre triangles formés sont isocèles rectangles. Les angles à la base valent 45° = .
Calcul pas à pas:

Retour Suite	Angles orientés en première Trigonométrie
Voir	Anamorphoses Droites Fractales Géométrie – Index Géométrie – Vue d'ensemble Homothétie – Débutant Mathématiques Théorème de Thalès en action Transformation du boulanger Transformations Triangles– Index
Aussi	DicoMot DicoNombre Théorie des nombres – Index Jeux, énigmes – Index Humour et pensées – Index
Cette page	http://villemin.gerard.free.fr/GeomLAV/Bases/AnglorEx.htm