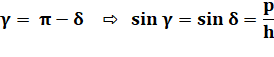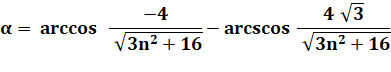|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
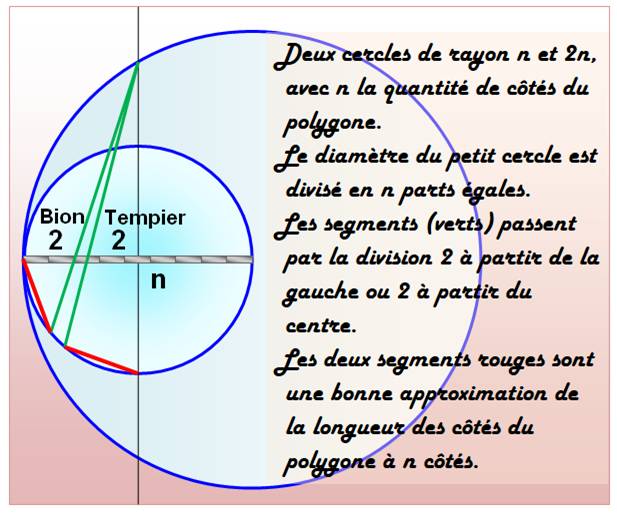
Partage du cercle en n parties égales ou Construction du polygone
régulier à n côtés Méthode Bion et méthode Tempier Méthodes
générales de construction des polygones à n côtés. Elles étaient utilisées
par les architectes et les artistes. On sait
qu'il n'existe pas de méthode générale de construction à la règle et au compas pour
tout type de polygone régulier. Seuls certains sont constructibles.
Ici, il
s'agit d'une méthode générale quelle que soit la quantité de côtés, au prix
d'une approximation plus ou moins importante que nous allons quantifier. Nicolas Bion
(1652-1733) est un ingénieur et
cosmographe français, constructeur d'instruments de mathématiques pour Louis
XIV. Auteur de: Traité de la construction et des principaux usages des
instrumens (sans t) de mathématiques (1709). Voir texte in fine >>> |
|
|
||
|
Procédé 1.
Choisir un segment BC marqué d'autant d'intervalles que n, la quantité
de côtés du polygone à construire. Ici, 9 pour un ennéagone. 2.
Cercles (B, BC) et (C, CB) qui se coupent en F et F'. On trace FF' qui
est ainsi la perpendiculaire en A de BC. 3.
Choisir D à la deuxième marque (valable pour tout n). 4.
Droite FD qui coupe le cercle en G. 5.
CG est un côté de l'ennéagone et l'angle CAG est très voisin de 40°. 6.
Les sommets de l'ennéagone sont obtenus en reportant la longueur CG
sur la périphérie du cercle (cercles pointillés orange) |
|
|
|
|
||||
|
But Calculer
la valeur de l'angle a = CAG dans le cas général. On prend
r = AC = AB = 1, ce qui ne change pas la valeur des angles. Le
segment BC est divisé en n intervalles (ici, n = 9). Remarques Chaque intervalle mesure 2r / n = 2/n. De sorte que: On se souvient que d'après la construction: CF =
CB = 2. Avec AC = 1, on calcule (Pythagore): Quant à l'hypoténuse h
|
|
|||
|
Avec les angles La loi
des sinus pour le triangle ADG |
|
|||
|
Angle gamma
en fonction de l'angle delta |
|
|||
|
En remplaçant |
|
|||
|
Évaluation de l'angle alpha |
|
|||
|
Nous connaissons ces deux angles par leur sinus |
|
|||
|
Avec les valeurs de p et q |
|
|||
|
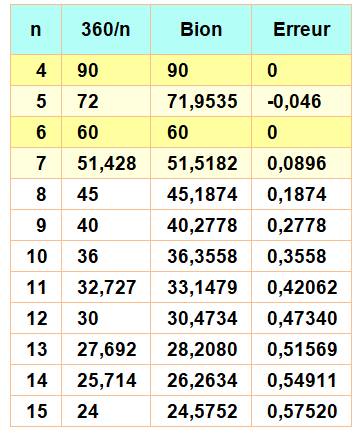
Application numérique Construction exacte pour les carrés et les
hexagones. Construction dont la précision diminue avec la
quantité de côtés. Zoom sur le point G
On constate bien ce décalage avec une
construction GeoGebra. Après report sur tout le cercle pour tracer les
sommets de l'ennéagone, le dernier cercle en pointillé coupe le cercle
origine en S avec 0,2 unité. |
|
|||
|
|
||||
|
Procédé Le même
que pour la méthode Bion jusqu'au tracé de demi-droite FD. Le point
D est choisi à deux intervalles à gauche du milieu du segment BC. GH est
alors un des côtés de l'ennéagone. |
|
|||
|
Formule |
|
|||
|
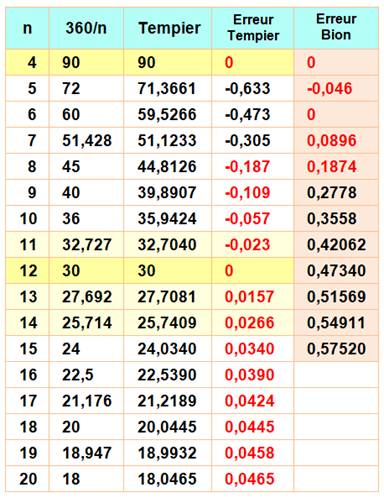
Application numérique Construction exacte pour les carrés et les dodécagones
et assez proche pour n autour de 12. Construction dont la précision diminue en
s'éloignant de 12 côtés. Les erreurs notées en rouge sont les plus petites
selon la méthode. Soit la conclusion:
D'autres informations sont disponibles sur le
site cité en référence. |
|
|||
![]()
|
|
|
|
Extrait du texte de Nicolas Bion Traité de
la construction et des principaux usages des instrumens de mathématiques –
Chapitre I page 19. Lecture
de la première ligne: Soit
proposé pour exemple à faire un Pentagone; si le cercle est donné, divisez
son diamètre A B en cinq parties égales par l'usage 8. Vous avez noté le
script de la lettre s de cette
époque. L'usage 8, fait référence à une méthode de construction n°8 décrite
lus haut dans le document..
La construction proposée du
pentagone
L'angle
au centre de 72° est approché par 71,95°, soit à 0,05° près (0,7‰). Pas mal
pour une construction aussi simple! |
|
Voir Construction exacte du pentagone
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()