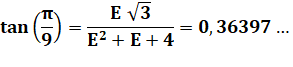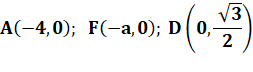|
||||||||||||||||||||||||||||||||||||||
![]()
|
Ennéagone – Nonagone Méthodes de construction L'ennéagone
régulier est inconstructible à la règle
et au compas. La
construction est faisable
avec une règle marquée et un compas (neusis). Il
est possible d'approcher de très près la construction précise de l'ennéagone. Pour
réaliser simplement un ennéagone, voir sa
construction à partir de l'hexagone en appliquant cette relation 9 = (3 x 6)
/ 2 |
|
|
||
|
1. Construire le tapis de rosaces
et le cercle qui les inscrit (bleu). 2. Du centre, tracer les trois demi-droites à 120° 3. Du point bas de la rosace centrale, tracer les deux droites roses,
puis la droite rose horizontale. 4. Les intersections avec le grand cercle sont les sommets de
l'ennéagone. |
|
|
|
|
||
|
5. Deux points A et B 6. Cercles (A, AB) et (B, AB) => points C et D 7. Point E quelconque sur AB 8. Cercle (E, AB) 9. Faire glisser E1 et son cercle le long de AB pour créer les intersections F et G 10. FG est un côté de l'ennéagone. 1 Mode opératoire (construction neusis): sur une
règle marquez le longueur du rayon et placer la règle passant par C et avec
les points E et F ajustés en position |
|
|
Comment s'y prendre pour la valeur de l'angle en F ?
|
Méthode
1: analytique. Elle est fastidieuse, mais permet de
découvrir les valeurs des sinus et cosinus de l'angle 20° >>> Méthode
1: géométrique. Avec quelques tracés supplémentaires, la
démonstration est immédiate; elle se lit directement sur la figure >>> |
|
|
|||
|
Notre but Justification avec les
lignes trigonométriques
de l'angle Pi/9 dont voici les
valeurs. Nous allons les calculer via la construction de l'ennéagone tout en
justifiant la construction. Notez que E est un nombre complexe. |
|
||
|
Note en passant Une approximation parfois utilisée pour approcher la construction de
l'ennéagone. |
|
||
|
Figure avec coordonnées La justification passe par
l'utilisation de la géométrie analytique: équations des cercles et de la droite pour trouver les coordonnées
des points d'intersection. Il s'agit de calculer
tan(CFD) = CD / CF.
|
|||
|
Avec
Pythagore |
|
||
|
Coordonnées
des points Avec FC
inconnu = a |
|
||
|
Équation de
la droite FD |
|
||
|
Équation du
cercle (A, AD) Équation
du cercle (F, FJ) |
|
||
|
Intersection
droite et cercles |
|
||
|
Résolution x1 vaut également 0 x2 vaut également la même chose avec (+8) au lieu
de (-8) pour le point symétrique. |
|
||
|
Intersection: x1 = x2 qui
permet de trouver la valeur de a. L'équation est horriblement
compliquée. Son graphe permet d'apprécier les racines. |
|
||
|
Un
logiciel de calcul donne la valeur la valeur exacte et son évaluation
numérique. On
vérifie la valeur de a sur la
figure du haut. |
|
||
|
Tangente de l'angle CFD: |
|
|
On pose E
et on calcule le cosinus. |
|
Voir Développements sur l'angle
Pi/9
|
|
||
|
Construction On trace AM perpendiculaire à AB et le segment
AJ. Démonstration Les triangles colorés sont isocèles et même équilatéral pour ABD. L'angle alpha en F se retrouve en A et son double
en J, puis en D.
Notez que l'angle MAJ
vaut 70° (90° – 20°). |
Figure illustrant une démonstration
quasi-muette
|
|
![]()
|
|
||
|
Construction très simple 1. Deux points A et B 2. Cercles (A, AB) et (B, AB) => points C et D 3. Droite CD 4. Segment OC = AM 5. Cercle (O, OA) 6. Report de la distance AB sur ce cercle => ennéagone approximatif. Calcul d'erreur Nous devons vérifier que l'angle ACB est très
proche de
40°. Nous avons R = AB = AC = BC = 1 (Le triangle ABC
est équilatéral): AC = 1 et AM
= 1/2
|
|
|
|
Calcul de la tangente et de l'arc tangente. Soit: 20,109 degrés au lieu des 20° attendus (0,5% d'erreur relative). |
|
|
|
|
||
|
1. Deux points A et B 2. Cercles (A, AB) et (B, AB) => points C et C' 3. Droite CB => D 4. Cercle (C,CC') => E 5. Cercle (E,EB) => F 6. DF est le côté de l'ennéagone (à très peu près). 7. Report de DF sur la périphérie du cercle bleu => 9 sommets de
l'ennéagone. |
|
|
|
|
||
|
Cette construction était connue d'Albrecht Dürer (Le manuel du
peintre). Construire cet hexagramme 1. Cercle de centre O de rayon R (vert pointillé). 2. Report du rayon R, six fois sur la circonférence (construction
de l'hexagone). 3. Dessin de l'hexagone et de ses prolongements (figure jaune). 4. Cercle (vert) inscrivant la figure jaune. |
|
|
|
5. Segment HP qui va devenir le rayon du cercle inscrivant l'ennéagone. 6. Cercle (H, HP) => deux points verts, deux sommets de l'ennéagone. |
|
|
|
7. Deux autres cercles de même diamètre centrés sur les deux autres
points orange. 8. Ligne joignant tous les points verts qui forme l'ennéagone régulier
complet. En fait une approximation |
|
|
|
Dans l'ennéagone
exact, l'angle ROT mesure 40°. Avec le dessin
de l'hexagone, on sait que l'angle ROS vaut 30°. Reste à
calculer l'angle SOT qui devrait approcher les 10°. Il nous
faut connaitre le rayon HP des cercles et leur équation pour calculer les
coordonnées du point d'intersection T. En prenant PQ, le côté de l'hexagone égal à 1. Le triangle OPQ est équilatéral et OP = 1. Alors: PH' = 1/2 H'O = cos(30°) HH' = 2 cos(30°) = |
|
|
Théorème
de Pythagore dans le triangle HPQ: |
|
|
Équation
du cercle vert de centre O (0, 0) et de rayon égal à HH': |
|
|
Équation du cercle bleu pointillé de centre H (0, |
|
|
Calcul en remplaçant x par sa valeur: |
|
|
Calcul de l'angle de en passant par sa tangente: |
|
|
La valeur de d par l'arc tangente: |
Sur
la calculette de votre ordinateur
Faire:
35 / Racine / 1 sur x / tan-1 (utilisez la flèche |
|
Comparaison: valeur de l'angle TOT comparé à 40° attendus: |
E =40 – 30 – 9,5940 = 0,406 … degrés E% = 1,01% En fait 3,65° sur l'ensemble des 9 valeurs. |
|
Il
existe d'autres constructions qui tentent d'approcher au mieux les 40° dont
celle qui utilise cette très bonne approximation:
Ne
pas oublier la méthode générale de construction des polygones dite Bion et Tempier. Erreur de seulement 0,1° pour
le cas Tempier. Voir
en référence un site proposant la construction au millième de degré près et
même moins. |
Voir Angles en Pi/9
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/EnneaCon.htm
|
![]()