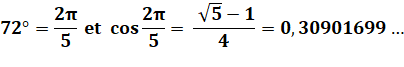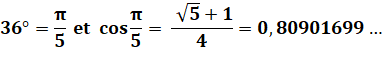|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PENTAGONE RÉGULIER – Constructions Première page consacrée à la
construction du pentagone régulier avec des outils informatiques. Les pages suivantes aborderont les différentes méthodes
de constructions à la règle et au compas. |
|
|
||
|
Dessiner
un côté AB du pentagone à la longueur désirée. Avec un
rapporteur centré sur le point A, dessinez une droite passant par la
graduation 108. Faites la
même chose à partir du point B. Ouvrir un
compas d'un écartement égal à AB Dessinez
le cercle de centre A qui coupe la droite bleue en E; dessinez le cercle de
centre B qui coupe l'autre droite bleue en C. Intersection en D. Pentagone régulier: ABCDE |
|
|
|
|
||
|
Principe Tracer les diagonales (pointillés bleus) qui
mesurent environ 1,62 fois la longueur du côté. Approximation du nombre
d'or: 1,61803398… Matériel Une corde avec une marque à 1 mètre et une autre
à 1,62 m (ou respectant cette proportion). Construction Segment AB de longueur 1 (par exemple). Cercles en A et B de rayon 1,62. Intersection C. Cercles unités en A et B. Intersection D et E Le polygone ABCDE est un pentagone approché. Précision Le sommet en C se trouve à 0,002 m (2 mm) plus
haut que pour le pentagone parfait. Précision largement suffisante en pratique; sinon
prendre 1,618 pour obtenir un écart de 0,000035 (35 microns). |
Pentagone quasi-régulier
AC = BC = 1,62 AB |
|
|
|
||
|
Je
rappelle que GeoGebra est un outil
gratuit et simple à utiliser. Vous
pouvez construire le pentagone comme pour la méthode manuelle à titre
d'exercice. Mais,
heureusement un tel logiciel permet la construction automatique de tout
polygone régulier. L'illustration ci-dessous montre l'outil à utiliser:
|
|
|
|
Note: la plupart des logiciels comme Word offre la possibilité de tracer
directement le pentagone. |
|
|
|
|
||
|
Méthode dite de Ptolémée Un
segment MN. Son milieu P et Q le milieu de PN. Cercle de
centre P et de rayon PN. Un
diamètre perpendiculaire à MN. Intersection
avec le cercle en D. Cercle de
centre Q et de rayon QD. Intersection
en R avec MN. La
longueur du segment DR est celle du côté du pentagone. Ouvrir le
compas avec cet écartement et reporter cinq fois (quatre suffisent) cette
longueur sur la circonférence du cercle. Pentagone
régulier: ABCDE. |
|
|
Voir Méthode expliquée, justifiée et variantes
|
|
||
|
Les
perpendiculaires aux côtés issues des sommets se coupent toutes au centre. Il suffit
d'en tracer deux pour désigner le point central. Notez que le point P est le même que celui utilisé pour la construction (ligne
pointillée rose). Le point
P est le centre du cercle circonscrit
et également du cercle inscrit.
Voir formules de calcul
des rayons |
|
|
|
clés
de la construction du pentagone régulier |
|
||
|
Construire la racine de 5, puis le
nombre d'or Le nombre
d'or (phi) est niché dans le pentagone: les diagonales mesurent phi fois
la longueur du côté.
Voir Construction
géométrie des nombres / Construction dorée par
Euclide |
Théorème de
Pythagore: (1 + 1)² + 1² = 5 |
||
|
Bissectrice des triangles isocèles Les diagonales trisèquent les angles
au sommet: trois angles de 36°. Le pentagramme présente trois triangles
isocèles d'or dont l'angle à la base (72°) est le double de l'angle au
sommet (36°). Conséquence: une des diagonales bissecte
l'angle à la base des triangles isocèles.
|
|
||
Voir Lignes
trigonométriques de Pi/5
|
|
|||||
|
Méthodes Consignes |
Racine de 5* |
Bissectrices |
Cercles |
Approchées |
|
|
Inscrire le pentagone dans un cercle |
|
|
6 – Cercle tangent 7 – Cercle tangent 9 – Avec des cercles |
|
|
|
Côté du pentagone imposé** |
|
|
|
||
|
Nombre d'or |
|
|
|||
* Les autres méthodes utilisent souvent
une construction de la racine de 5
**D'autres
méthodes sont décrites sur la page de Patrice
Debart en imposant la diagonale ou autres
Voir Une méthode
originale par coïncidence de points
Voir Constructions élémentaires / Construction de l'icosagone
|
|
||
|
Construire
d'abord deux pentagones et deux étoiles emboitées. Construire
les arcs de cercle à partir des quatre centres indiqués.
Formule: rayon du cercle circonscrit à la l'hexagone et la hauteur de l'œuf. R = 0,79719 … L |
Pour
info construction plus classique de l'œuf Cercle (rose) de centre O de rayon
R, puis de centre A et B avec un rayon 2R.
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/PentaCon.htm |
![]()
Renvois
de liens