Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 09/01/2024 M'écrire Brèves de Maths

INDEX Géométrie	Pavage du Plan
	Approche	Avec polygones	Apériodique	Pavage fini
	Triangles	Carrés parfaits	Rectangles	Penrose (losanges)
	Pentagone	Hexagone	Dodécagone	Disque (Pizza)
	Dominos	Échiquier	Plus Plus (Jeu)

Faites un double-clic pour un retour en haut de page

PAVAGE MONOTUILE APÉRIODIQUE David Smith est un mathématicien anglais amateur de 64 ans. En 2023, il trouve le moyen de paver le plan avec une seule tuile sans qu'aucun motif ne se répète (pavage apériodique). Non seulement il montre que cette tuile existe, mais on en connait désormais un exemple.
	Sommaire de cette page >>> Le	Débutants pavage Glossaire Géométrie

Anglais: aperiodic tiling, an aperiodic monotile

Pavage monotuile apériodique: résolu		haut
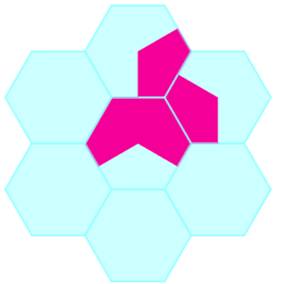
Problème Est-il possible de paver parfaitement un plan d'un unique motif, de manière apériodique ? Sans trou et sans motifs qui se répètent. Pavage périodique (ou régulier) Un carrelage classique fait de carrés ou d'hexagones produit un motif périodique, un dessin qui se répète. Dans le cas périodique, une partie du pavage peut être découpée et elle pourra être superposée parfaitement à une autre partie du pavage. Pavage apériodique L'illustration montre un exemple de pavage apériodique trouvé par un passionné anglais David Smith. La non-périodicité a été prouvée par des chercheurs à l'aide d'ordinateurs (assistants de preuve).

Pavage périodique et apériodique		haut
Pavage périodique De façon intuitive, un pavage consiste à diviser un plan en morceaux sans espaces ni chevauchements. Les pavages périodiques possèdent une symétrie dite de translation. Imaginez un damier infini. Faites-le glisser d'une case vers le haut, chaque pièce s'inscrira toujours exactement dans le motif du damier.
Types de pavages

Pavage apériodique résolu			haut
Découverte Quatre chercheurs viennent de résoudre un vieux problème mathématique: le problème ein stein (une pierre, en allemand) Comment un plan peut-il être recouvert par une seule tuile sans répétition de motif. Une copie du pavage translatée ne trouvera jamais la possibilité d'une exacte superposition à moins de revenir à la position initiale. C'est David Smith qui a composé la tuile et Myers, Kaplan et Goodman-Strauss qui ont procédé aux vérifications.		Tuile à 13 côtés en forme de chapeau Pour paver le plan, il faut utiliser cette tuile-chapeau à l'endroit ou à l'envers.
Construction de la tuile

Historique

1961 – Hao Wang invente des tuiles particulières et conjecture que le pavage est forcément périodique.

1964 – Robert Berger, un de ses doctorants, infirme la conjecture en exhibant un ensemble de 20 426 tuiles différentes dont tous les pavages possibles sont apériodiques.

1971 Raphael Robinson descend à six tuiles.

Rapidement ce nombre est réduit à deux tuiles différentes. C'est Roger Penrose, dès 1970, qui propose un ensemble de deux tuiles qui ne permet que des pavages apériodiques.

2010 – Une monotuile apériodique est proposée, mais elle est composée de plusieurs morceaux déconnectés.

2023 – Smith et ses trois collaborateurs proposent "un chapeau pour Einstein".

Haut de page (ou double-clic)

Suite	Pavage avec pentagones Jeu du PLUS PLUS
Voir	Carré Carrés parfaits Construction géométrique des nombres Dodécagone Dominos Frises – Bandes décoratives Géométrie – Index Golygone à huit côtés	Carré Carrés parfaits Construction géométrique des nombres Dodécagone Dominos Frises – Bandes décoratives Géométrie – Index Golygone à huit côtés
Sites	Pavage apériodique – Wikipédia An aperiodic monotile – David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss
Cette page	http://villemin.gerard.free.fr/Pavage/Aperiodi.htm