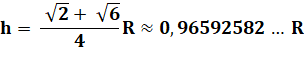dodécagone

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/12/2020 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Polygones
Débutants Géométrie	POLYGONES un par un										Glossaire Géométrie
INDEX Polygones Géométrie	Noms	-1-	-2-		-3-	-4-	-5-	-6-	-7-	-8-		-9-
	10	11	12		13	14	15	16	17	18		19
	20				23
				Sommaire de cette page >>> Dodécagone régulier >>> Mesures >>> Pavage du dodécagone >>> Triangles équilatéraux dans le dodécagone >>> Dodécagone régulier et ses diagonales >>> Diagonales du dodécagone – Calcul des longueurs

DODÉCAGONE

Polygone à douze côtés ou douze angles (du grec: duodeka, douze et gonia, angle).

Dodécaèdre régulier: 12 côtés égaux* et 12 angles de 150°. Il est constructible .

La pièce de 50 cents australienne est découpée selon un dodécaèdre régulier.

* On dit plutôt de même mesure ou de même longueur

Anglais: a dodecagon is a 12-sided polygon / regular dodecagon

Galerie de dodécagones

DODÉCAGONE RÉGULIER
Sommets	12
Droites	66 = 11x12/2
Côtés	12
Diagonales	54
Triangles	10 (avec diagonales issues d'un sommet)
Angle interne	150°
Somme des angles	1 800° = 180 (12-2)
Longueur du côté	a
Rayon du cercle Inscrit	r
Rayon du cercle circonscrit	R = a / 0,517 638 090 …
Apothème
Aire Voir Calcul de l'aire
Approximation de Pi	3, 105 828 …

MESURES dans le dodécagone

Le dessin montre 1/6 du dodécaèdre de côté AO'

Le segment AB serait le côté de l'hexagone.

Le triangle OAB est équilatéral.

OA = OO' = OB = AB = R

– Rayon du cercle circonscrit au dodécaèdre.

AO' = O'B = a

– Côté du dodécaèdre.

OH² = OA² - AH² = R² - (R/2)² = ¾ R²

OH = R

O'H = R (1 – )

AO'² = AH² + HO'² = (R/2)² + R² (1 – )²

= R² { (1/2)² + (1 – )² }

= R²/4 { (1)² + (2 – )² }

= R²/4 { 1 + 4 – 4 + 3 }

= R²/4 { 8 – 4}

= R² { 2 – }

a / R = 0, 517 638 090 205 041 524 70 …

Calcul approché de

Le rapport entre le périmètre du dodécagone 12a et son diamètre D = 2R donne 6 x 0,517… = 3,106 … = Pi₁₂, est une valeur approchée de .

Avec 24 côtés on trouverait un rapport de 0,261 052 38 et une approximation de qui vaut 12 fois cette valeur, soit: Pi₂₄ = 3,132 …

Un calcul trigonométrique avec un nombre de côté égal à n donne :

En fait Pi_n tend vers lorsque n tend vers l'infini.
Voici un tableau montrant la vitesse (lente) de convergence:

Diagonales du dodécagone

Voir Dénombrement des diagonales, intersections et régions

Pavage du dodécagone en douze parts

Pavage monohédral (en parts égales) du dodécagone avec des parties non centrales.

Les pointillés montrent la construction.

Les douze quadrilatères sont irréguliers, mais congruents (égaux, superposables).

Ils sont formés d'un triangle équilatéral adjacent à un triangle isocèle.

Voir Pavage du disque et autres

Un pavage possible avec un carré et deux triangles équilatéraux

(Déduit de celui présenté ci-dessus)

Proposé par Jean-Louis Breuil

Triangles équilatéraux dans le dodécagone

Notez les points d'intersection selon la taille des triangles équilatéraux.

Voir Calculs dans l'octogone

Dodécagone régulier et ses diagonales

Longueur de la diagonale k, avec k la quantité de côtés interceptés par la diagonale.

k	Longueur	Formule
2	1,931851652
3	2,732050807
4	3,346065216
5	3,732050808
6	3,863703305

Voir Son calcul / Tables / Quantité d'intersections des diagonales

Diagonales du dodécagone – Calcul des longueurs
Exercice de géométrie Angle au sommet interceptant un côté Diagonales d1 = AG = D d2 = AF d3 = AE d4 = AD d5 = AC Rayon des cercles circonscrit: MA = R = D/2 inscrit: MO = r Apothème MO = r Calculs des longueurs pour une longueur du côté: a = 10.
Grande diagonale d1 = AG, diamètre du cercle circonscrit (D):
Deuxième diagonale d2 = AF = BG:
Petite diagonale d5 = AC:
Rayon du cercle inscrit, apothème: r = OM = AP
Quatrième diagonale d4 = AD:
Troisième diagonale d3 = AE:

Suite	Dodécagone – Construction Dodécaèdre Heptadécagone
Voir	Polygone Hexagone Calcul de Pi Partage du cercle en parts égales
Aussi	Constructibilité Géométrie – Index Partage du cercle Rosaces
DicoNombre	Nombre 12 Nombre 0,517
Cette page	http://villemin.gerard.free.fr/GeomLAV/Polygone/Dodeca.htm