|
||||||||||||||||||||||||||
![]()
|
NOMBRES VAMPIRES Nombre dont les chiffres
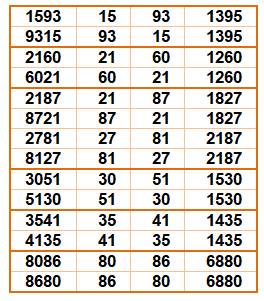
sont arrangés en un produit qui redonne le nombre. Ex: 1260 = 21 x 60 |
Anglais: Vampire number
The
vampire numbers were introduced by Clifford A. Pickover in 1994
|
|
|||||
|
On élimine le cas des multiples zéros à droite |
|||||
|
4 chiffres 7 nombres vampires |
Aucun n'est premier |
||||
|
5 chiffres 0 nombre vampire |
Par
définition |
||||
|
6 chiffres: 148 nombres vampires |
Exemples 108135 = 135 x 801 129640 = 140 x 926 118440 = 141 x 840 136948 = 146 x 938 105750 = 150 x 705 … 516 879 = 681 x 759 Voici les 5 nombres
vampires PREMIERS 117067 = 167 x 701 124483 = 281 x 443 146137 = 317 x 461 371893 = 383 x 971 536539 = 563 x 953 |
||||
|
8 chiffres 3 228 nombres vampires |
Voici le début de
liste 10025010 = 5010 x 2001 10042510
= 4001 x 2510 10052010
= 5001 x 2010 10052064
= 5016 x 2004 10081260
= 8001 x 1260 Etc. |
||||
|
10 chiffres 108 454 nombres vampires |
Voici le début de
liste 1000174288 1000191991 1000198206 1000250010 Etc. |
||||
|
Dans l'ordre croissant (Référence
Sloane A014575) |
|
||||
Anglais : Pairs of trailing zeros are not
allowed
|
|
||
|
DOUBLEMENT Le plus petit Le seul à 6 chiffres |
125460 = 204 x
615 = 246 x
510 |
|
|
Le suivant: 8 chiffres |
12054060
= 2004
x 6015 = 2406
x 5010 |
|
|
TRIPLEMENT Le plus petit Le seul à 8 chiffres |
13078260
= 1620
x 8073 = 1863
x 7020 = 2070
x 6318 |
|
|
Le suivant: 12 chiffres Il y en a 13 à 12 chiffres |
107650322640 =
140532 x 766020 =
153204 x 702660 =
200760 x 536214 |
|
|
QUADRUPLEMENT Le plus petit |
16758243290880 =
1982736 × 8452080 =
2123856 × 7890480 =
2751840 × 6089832 =
2817360 × 5948208 |
|
Anglais: Vampire numbers having three
distinct pairs of fangs
|
|
||
|
|
126 = 6 x 21 153 = 3 x 51 688 = 8 x 86 1206 = 6 x 201 1255 = 5 x 251 1260 = 6 x 210 1395 = 5 × 9 × 31 114390 = 31 x 41 x 90 197925 = 29 x 75 x 91 |
|
|
|
||
|
Alors N et a + b donne le même résultat en appliquant
la preuve par neuf.
|
Exemple 1435 =
35 x 41 1 + 4 +
3 + 5 = 4 mod 9 35 + 41
= 3 + 5 + 4 + 1 mod 9 |
|
Le
produit des deux couples de chiffres
donne
les chiffres, mais pas dans l'ordre.
![]()
|
Suite |
|
|
Voir |
|
|
Site |
Vampire
numbers Walter Schneider |
|
Cette page |
![]()
