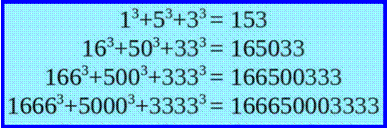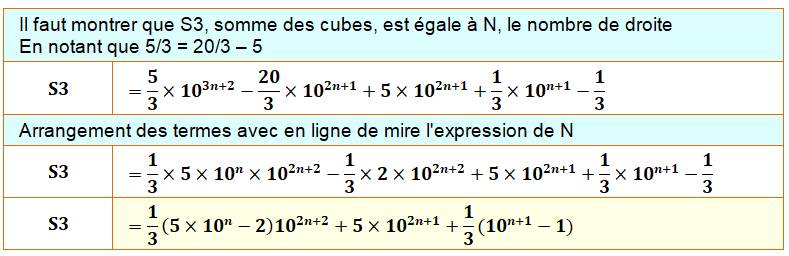NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/11/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres en forme
Débutants Général	Somme des chiffres				Glossaire Général
INDEX Narcissiques Somme-Produit Ch Formes et motifs Nombres en chiffres Chiffres Types de nombres Jeux et énigmes Puissance Décomposition	Sommes des chiffres		Racine numérique	Cycle des carrés
	Sommes des Ch de n^k		Narcissique	k-narcissiques
	Digipuissants		Armstrong	Puissances consécutives
			Faute de frappe
		Sommaire de cette page >>> Les cousins >>> Nombres narcissiques >>> Cas de 153, 165033, … >>> Liste de 88 nombres narcissiques >>> Cycle narcissique d'ordre 3 >>> Quelques cycles >>> Records

NOMBRES NARCISSIQUES

ou

NOMBRES D'ARMSTRONG

NOMBRES DIGIPUISSANTS

NOMBRES EXPOSANTS

EXPOSITORY NUMBERS

Nombre n formé des chiffres a, b, c tel que, par exemple:

n = a³ + b³ + c³

Anglais: Narcissistic number, Armstrong number, perfect digital invariant or plus perfect number.

Puissances et chiffres – Les cousins
Résumé (les carrés représentent les chiffres du nombre)

Friedman	Nombre dont les chiffres calculés redonnent le nombre. >>> * Friedman multiplicatif.	25 = 5^2 126 = 21 x 6* 343 = (3 + 4)^3
Friedman sauvage	Nombres de Friedman faisant appel à des opérateurs non classiques >>>

Narcissiques	Nombre égal à la somme de ses chiffres à une puissance. >>>	153 = 1^3 + 5^3 + 3^3
Armstrong	Narcissiques avec autant de termes que la puissance >>>	1 741 725 = 1^7+7^7+4^7+1^7+7^7+2^7+5^7 Sept termes pour une puissance 7.
Digipuissants (Dudeney)	Nombre égal à la puissance énième de la somme de ses chiffres >>>	512 = (5 + 1 + 2)^3
K-Narcissiques	Nombre égal k fois la somme de ses chiffres à une puissance. >>>	702 = 2 (7^3 + 0^3 + 2^3) = 2 (343 + 8) = 2 x 351
P-Narcissique Narcissiques puissants	Nombre égal à la somme des chiffres porté à des puissances successives. >>>	518 = 5^1 + 1^2 + 8^3 Variantes 3 435 = 3^3 + 4^4 + 3^3 + 5^5 …
Expository (Narcissiques de Keith)	Nombre égal à une combinaison des sommes des chiffres du nombre, du carré, du cube, etc. et, dans chaque cas, mis à une puissance particulière. >>>	336 = 3 + 3 + 6 + 3^2 + 3^2 + 6^2 + 3^3 + 3^3 + 6^3

Narcissiques Produits	Nombre faute de frappe Nombre égal au produit-puissances successifs de ses chiffres. >>>	2592 = 2^5 x 9^2
Narcissiques Fractions	Nombres égaux à une fraction avec chiffres à une puissance au numérateur comme au dénominateur >>>
Narcissiques inverses	Nombre égal à la somme d'un nombre à puissance successive de ses chiffres. >>>	1 033 = 8^1 + 8^0 + 8^3 + 8^3 4 624 = 4^4 + 4^6 + 4^2 + 4^4
SOCHIPUIS	Nombre égal à la somme de ses chiffres portés à une puissance >>>	89 = 8^1 + 9^2 1 034 = 1^1 + 0^1 + 3^2 + 4^5
NESCHIP	Nombre Égal à la Somme des CHIffres portée à une Puissance (sigle). >>>	512 = 8^3 & 5 + 1 + 2 = 8
Kaprekar	Nombre égal à la somme des parties droite et gauche portée à une puissance. >>>	2025 = 45^2 & 20 + 25 = 45

Voir Somme-Produit des chiffres – Toutes les autres possibilités

NOMBRES NARCISSIQUES
Définition Nombre égal à la somme de ses n chiffres chacun élevé à la puissance n. Les vrais narcissiques sont ceux k chiffres avec la puissance k. Exemples
1 =	1^1	10 cas: Tous les chiffres
n =	a^2 + b^2	0 cas
153 =	1^3+ 5^3+ 3^3
370 =	3^3+ 7^3+ 0^3	4 cas
371 =	3^3+ 7^3+ 1^3
407 =	4^3+ 0^3+ 7^3
1 634 = 8 208 = 9 474 =	1^4+ 6^4+ 3^4+ 4^4 8^4+ 2^4+ 0^4+ 8^4 9^4+ 4^4+ 7^4+ 4^4	3 cas
4150 = 4151 = 54 748 = 92 727 = 93 084 = 194 979 =	4^5+ 1^5+ 5^5+ 0^5 4^5+ 1^5+ 5^5+ 1^5 5^5+ 6^5+ 3^5+ 4^5+ 8^5 9^5+ 2^5+ 7^5+ 2^5+ 7^5 9^5+ 3^5+ 0^5+ 8^5+ 4^5 1^5+ 9^5+ 4^5+ 9^5+ 7^5 + 9^5	2 cas (4 chiffres à la puissance 4) – dits Armstrong de quatrième espèce. + 4 cas vrais (5 chiffres à la puissance 5) – dits Armstrong de première espèce.
548 834 =	5^6+ 4^6+ 8^6+ 8^6+ 3^6+ 4^6	1 cas
1 741 725 = 4 210 818 = 9 800 817 = 9 926 315 = 14 459 929 =	1^7+ 7^7+ 4^7+ 1^7+ 7^7+ 2^7+ 5^7 = 1 + 823 543 + 16 384 + 1 + 823 543 + 128 + 78 125 Etc.	5 cas
24 678 050 = 24 678 051 = 88 593 477 =	= 2^8 + 4^8 + 6^8 + 7^8 + 8^8 + 0^8 + 5^8 + 0^8 Etc.
146 511 208 =	…

Nombres d'Armstrong Il y a exactement 88 nombres narcissiques vrais (ou Armstrong). Le plus grand a 39 chiffres. Voir Explications et liste

Programme Maple

Commentaires Réinitialisation du logiciel. Lancement de la boucle d'analyse des nombres n. Conversion de n en N, la liste des chiffres de n avec q la quantité de chiffres. Calcul de la somme des chiffres de n à la puissance égale à la quantité de chiffres (q). Si cette somme (S) est égale à n, alors on imprime la liste. Fin de boucle (od, qui est le do à l'envers). En bleu, le résultat du traitement pour la plage spécifiée pour n

Voir Somme des puissances des chiffres  / Narcissiques en couple / Boucles en cubes

Voir Programmation – Index

Cas de 153, 165033, …
Cette suite d'égalité est infinie. Voir Brève 689 / Nombre 153 Voyons pourquoi en examinant chaque nombre.

CYCLE NARCISSIQUE d'ordre 3

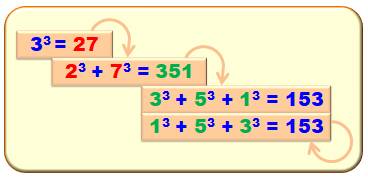
Cycle

Le cycle consiste à calculer la somme des cubes des chiffres d'un nombre puis la somme des cubes des chiffres de cette somme; etc.

Exemple pour 2

2	Somme des cubes des chiffres
8	8
512	125 + 1 + 8 = 134
134	1 + 27 + 64 = 92
92	729 + 8 = 737
737	343 + 27 + 343 = 713
713	343 + 1 + 27 = 371
371	Mêmes chiffres, soit même total

Ici, le cycle narcissique du 2 se termine par le nombre narcissique 371.

Exemple avec 3

Voir Brève de maths 210 / Procédé itératif de Kaprekar

Anglais: The digit cube sum problem

Quelques cycles avec la somme des chiffres au cube
Propriété Tous les nombres divisibles par 3 ont un cycle qui se termine par 153. La table à droite montre quelques exemples: le nombre de départ, les sommes successives et la longueur du cycle. Voir aussi Tableau Excel Records: nombre de départ, quantité de cycle, [cycle] 3, 3, [27, 351, 153] 6, 10, [216, 225, 141, 66, 432, 99, 1458, 702, 351, 153] 117, 11, [345, 216, 225, 141, 66, 432, 99, 1458, 702, 351, 153] 177, 13, [687, 1071, 345, 216, 225, 141, 66, 432, 99, 1458, 702, 351, 153] 12 558, 14, [771, 687, 1071, 345, 216, 225, 141, 66, 432, 99, 1458, 702, 351, 153] Aucun cycle plus long jusqu'à cent millions. Résultat de mon test en environ une heure de calculs. Shyam Sunder Gupta indique que l'on atteint 15 avec le nombre 44499999999999999999 = 43917.

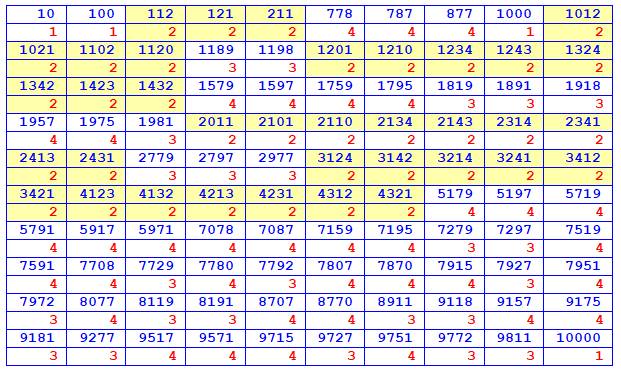
Exemple avec les premiers nombres

En tête de colonne, le nombre de départ (de 1 à 20).

En jaune, arrêt sur un nombre narcissique.

En rose, boucle

En rouge, nombre déjà rencontré dans les colonnes précédentes.

Notes:

Le nombre 13 fait apparaître un cycle avec 133. Les ésotéristes y voient une signification. Le nombre 153 est aussi important pour eux.

Cycle narcissique aboutissant à 1

Tous les nombres jusqu'à 10 000 dont le cycle se termine par 1 et la quantité nécessaire de boucle

La somme 1 du premier coup est triviale pour les puissances de 10.

En deux cycles, on trouve tous les nombres dont la somme des chiffres est une puissance de10. Ex: 1234 => 1³ + 2³ + 3³ + 4³ = 1 + 8 + 27 + 64 = 100.

Le plus petit nombre exigeant 5 itérations est 13 477 et les suivant (hors permutations) est 17 779.

Quelques cycles particuliers

La somme des cubes des quatre premiers chiffres est égale à 100.

Tous les repdigit, comme tous les multiples de 3, ont un cycle narcissique qui aboutit à 153.

Cycles doubles ou triples

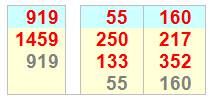
Le nombre 919 donne un cycle narcissique à 2 nombres

Le nombre 55 donne un cycle narcissique à 3 nombres

Etc.

Puissance	Départ	Suite	Quantité
2	4	4, 16, 37, 58, 89, 145, 42, 20.	8
3	55	133, 55	2
	136	244, 136	2
	160	217, 352, 160	3
	919	1459, 919	2
4	1138	4179, 9219, 13139, 6725, 4338, 4514, 1138	7
	2178	6514, 2178	2

Records de cycles 3-narcissiques dont les nombres sont tous différents

Longueur du cycle, CYCLE, altitude maximale

8, [2, 8, 512, 134, 92, 737, 713, 371] – 512

11, [6, 216, 225, 141, 66, 432, 99, 1458, 702, 351, 153] – 1 458

12, [68, 728, 863, 755, 593, 881, 1025, 134, 92, 737, 713, 371] – 1 025

14, [177, 687, 1071, 345, 216, 225, 141, 66, 432, 99, 1458, 702, 351, 153] – 1 458

15, [12558, 771, 687, 1071, 345, 216, 225, 141, 66, 432, 99, 1458, 702, 351, 153] – 12 558

Fin, à ma connaissance !

Énigme

Quatorze voitures d’une grande administration sont rangées l’une derrière l’autre sur le parking officiel de la Préfecture. Je remarque qu’elles portent toutes un numéro d’immatriculation différent, inférieur à 1500, mais aussi, chose étonnante, que le numéro de chacune est égal à la somme des cubes des chiffres du numéro de la voiture placée devant elle. Quel est le numéro de la cinquième voiture ?

Réponse par lecture de la liste ci-dessus: 177, 687, …

Énigme communiqué par Roger Rigaud

Voir Brève 844

Suite	Somme des carrés des chiffres Somme des chiffres des puissances Nombres de Dudeney Monstre de Taneja Somme-Produit des chiffres – Index
Voir	Automorphiques Facteurs sans zéro Nombres et puissances de leurs chiffres Palindromes Pannumériques Partition en puissance
Site	Nombres narcissiques – Tangente – Gianni Sarcone Nombre narcissique – Wikipédia Narcissistic number – Wolfram MathWorld Narcissic numbers – Harvey Heinz A brief introduction to Armstrong numbers – M.F. Armstrong – Définition des quatre espèces OEIS A005188 – Armstrong (or Plus Perfect, or narcissistic) numbers: m-digit numbers equal to sum of m-th powers of their digits (a finite sequence, the last term being OEIS A098870 – Sum of the cubes of the digits of the previous term, starting with 2 The Digits Cube Sum Problem
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Formes/Narcissi.htm