|
||||||||||||||||||||||||||
![]()
|
ou Nombres colombiens Nombres
non-accessibles par un autre en lui ajoutant ses chiffres. Trouvés par Kaprekar
en 1949. Sinon, comme 100, ce n'est pas un auto-nombre.
Mais avec deux sommes ou plus, il s'agit d'un nombre jonction. |
Anglais: self number or Colombian number or Deviali number
|
|
||
|
15 = 12 + 1 + 2 |
Le
nombre 15 est la somme de
Peu
importe ce nombre, Pourvu
qu'il en existe un. |
|
|
20 = ? |
Impossible
d'atteindre 20 pas ce même procédé. |
|
|
Plusieurs fois |
Le
plus petit somme deux fois (nombre jonction). 101 = 91 +
10 = 100 + 1 Le
plus petit trois fois est assez grand: 10 000 000
000 001 = 9 999 999 999 892 + 109 = 9 999 999 999 901 + 100 = 10 000
000 000 000 + 1 Le
plus petit quatre fois: 1 000 000
000 000 000 000 000 102 avec {2, 11, 200 et 209} |
|
|
|
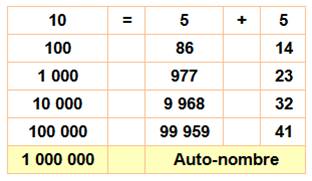
Anecdote: Kaprekar signale
que le millionnaire est un VIP car un million est la première puissance de 10
auto-nombre. La suivante est 1016. |
|
|
Quantité |
Infinie. |
|
"Chiffre-addition" (Anglais:
Digitadition terme inventé par Kaprekar) |
Nombre n additionné de la somme de ses
chiffres. d(12) = 12 + 1 + 2 = 14 d(123) = 123 + 1 + 2 + 3 = 129 Un
auto-nombre est un nombre non atteint par une chiffre-addition. |
|
Chiffre-addition récurrente, une manière de créer tous les autonombres |
Le
procédé de chiffre-addition peut être répété au nombre trouvé: 100, 101, 103, 107, 115, 122, 127, 137, 148, 161, 169, 185, 199, 218,
229, 242, 250, 257, 271, 281, 292 … Suite
en puissance de 2 qui avorte … 1, 2, 4, 8, 16, 23, 28, 38, 49, 62, 70, 77, 91, 101, 103, 107, 115,
122, 127, 137, 148 Nombres
de 1 à 50
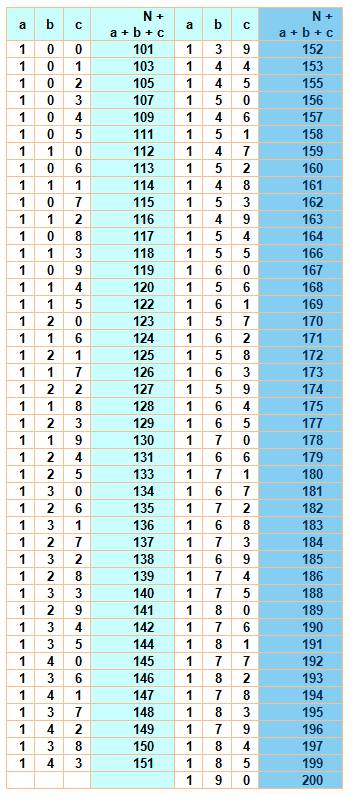
Les
nombres en tête de colonne (bleus)
engendrent tous les auto-nombres de la colonne. Ces nombres qui ne se
retrouvent pas dans les colonnes des autres, qui n'ont pas de générateurs, sont auto-nombres.
|
|
Une formule |
Cette
formule de récurrence avec C1 = 9, produit certains autonombres.
C1 = 9 C2 = 8 x 102-1 + 9 + 8 = 97 |
|
|
||
|
Pour
voir "en gros" Visualisation
du procédé pour donner un aperçu. Lisez sans trop chercher à comprendre. Vous
pourrez y revenir après avoir lu l'explication détaillée plus bas.
Explication
détaillée sur un exemple |
||
|
Nombre N à tester: |
3 333 333 333 |
|
|
Somme des chiffres. Renouvelée (comme pour la preuve par 9). |
3 + 3 +…+ 3 = 10 x 3 = 30 3 + 0 = 3 |
|
|
Division par 2, avec addition préalable de
9 si impair. |
(3 + 9) / 2 = 6 |
|
|
Soustraction de N. |
3 333 333 333 – 6 = 3 333
333 327 |
|
|
Générateur de N. |
3 + 3 + … + 7 = 24 + 9 =
33 3 333 333 327 + 33 |
|
|
On recommence en enlevant 9 autant de fois
que de chiffres dans N. La somme n'est jamais égale à N, alors N
est un auto-nombre. |
3 333 333 318 + 33 = 3
333 333 351 3 333 333 309 + 33 = 3
333 333 342 3 333 333 300 + 24 = 3
333 333 324 3 333 333 291 + 33 = 3
333 333 324 3 333 333 282 + 33 = 3
333 333 315 3 333 333 273 + 33 = 3
333 333 306 3 333 333 264 + 33 = 3
333 333 297 3 333 333 255 + 33 = 3
333 333 288 3 333 333 246 + 33 = 3
333 333 279 |
|
|
Prenons
un nouveau nombre. |
3 333 333 334 Somme chiffres: 31, puis 4 Division par 2 (pair) =>
2 |
|
|
Soustraction avec 2. Puis itérations avec -9. La quatrième itération donne N, ce nombre
n'est pas auto-nombre puisque cette dernière chiffre-addition donne N.
Autrement-dit, N a un générateur. |
3 333 333 332 + 31 = 3 333 333 362 3 333 333 323 + 29 = 3 333 333 352 3 333 333 314 + 29 = 3 333 333 343 3 333 333 305 + 29 = 3
333 333 334 |
|
D'après un exemple donné
par Malcom E. Lines
![]()
|
|
|||
|
Nombre |
Auto-nombre |
Pas auto-nombre (jonction) |
|
|
1 |
1 |
|
|
|
2 |
|
1 + 1 |
|
|
3 |
3 |
|
|
|
4 |
|
2 + 2 |
|
|
5 |
5 |
|
|
|
6 |
|
3 + 3 |
|
|
7 |
7 |
|
|
|
8 |
|
4 + 4 |
|
|
9 |
9 |
|
|
|
10 |
|
5 + 5 |
|
|
11 |
|
10 + 1 + 0 |
|
|
12 |
|
6 + 6 |
|
|
13 |
|
11 + 1 + 1 |
|
|
14 |
|
7 + 7 |
|
|
15 |
|
12 + 1 + 2 |
|
|
16 |
|
8 + 8 |
|
|
17 |
|
13 + 1 + 3 |
|
|
18 |
|
9 + 9 |
|
|
19 |
|
14 + 1 + 4 |
|
|
20 |
20 |
|
|
|
21 |
|
15 + 1 + 5 |
|
|
22 |
|
20 + 2 + 0 |
|
|
23 |
|
16 + 1 + 6 |
|
|
24 |
|
22 + 2 + 2 |
|
|
25 |
|
17 + 1 + 7 |
|
|
… |
|
|
|
|
|
|||
|
Les premiers auto-nombres
Il y en a une
infinité, quelle que soit la base. Remarquez l'écart général de
11 entre eux. Mais, il y a des exceptions (97 à 108 par exemple). Anglais: we note that
each number is just 11 larger than its predecessor. Is this how the larger
self-numbers are obtained in general? Not quite! Although most self-number do
follow this pattern, occasionally there comes a break in the pattern which
adds interest to what otherwise would be a rather dull exercise. Voir Anglais Auto-nombre premiers
|
|||
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()