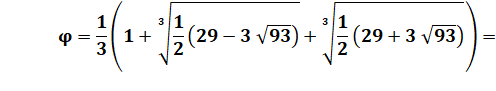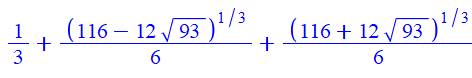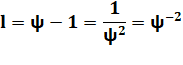|
Édition du: 08/01/2024 |
|
INDEX |
Nombre d'or |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
SUPER NOMBRE d'OR Il existe trois
constantes résultant de la convergence du ratio de deux nombres successifs
pris dans les suites de Fibonacci,
Padovan
et Narayana. Leur valeur et l'équation dont elles sont
racines.
|
|||||||||||
|
|
Sommaire de cette page >>> Suite de Narayana >>> Nombre d'or et super nombre d'or >>> Valeurs >>> Relations >>> Super nombre d'or en géométrie |
Débutants Glossaire |
|||||||||
Anglais: supergolden ratio / hypergolden ratio
/ Narayana sequence / Narayana's cows
|
Définition de la suite Comme pour la suite de Fibonacci, on définit les
points de départ et la récurrence: A0 = 0; A1 = 1; A2
= 1; A3 = 1; AN+1 = AN-1 + AN-3 |
Nombre de la suite 1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60, 88, 129, 189, 277, 406, 595,
872, 1278, 1873, 2745, 4023, 5896, 8641, 12664, 18560, 27201, 39865, 58425,
85626, 125491, 183916, 269542, 395033, 578949, 848491, 1243524, 1822473,
2670964, 3914488, 5736961, 8407925, … |
|
|
Lapins et vaches La suite de Fibonacci compte la population des
lapins selon les générations. Celle de Narayana, celle des vaches et des veaux. |
Quelle est la population de la énième génération
de vaches et veaux, sachant que chaque vache donne naissance à un veau par an
à partir de l'âge de trois ans ? Le énième nombre de Narayana est aussi la
quantité de compositions
de n en 1 et 3 éléments. |
|
Voir Nombres de Narayana
/ Brève 56-1117
|
|
NOMBRE D'OR |
SUPER NOMBRE D'OR |
|
|
Ratio |
Le ratio de deux nombres consécutifs de la suite
de Fibonacci converge vers le nombre d'or. |
Le ratio de deux nombres consécutifs de la suite
de Narayana converge vers le SUPER nombre d'or. |
|
|
Valeur |
|
|
|
|
|
1,6180339887 4989484820 4586834365 6381177203
0917980576… |
1,4655712318 7676802665 6731225219 9391080255
7756847228… |
|
|
Rapport |
Deux valeurs a > b > 0 sont dans le rapport
doré si:
|
Deux valeurs a > b > 0 sont dans le rapport
super doré si:
|
|
|
Équation |
x2 = x + 1 |
x3 = x2
+ 1 |
|
|
Racines |
1,61803398… – 0,618033988… |
1,465571232 – 0,232785615… + 0,792551993… i – 0,232785615… – 0,792551993… i |
|
Voir Nombre
plastique et suite de Padovan avec x3 = x + 1
|
Valeur exacte du nombre
Fraction continue du super nombre
d'or
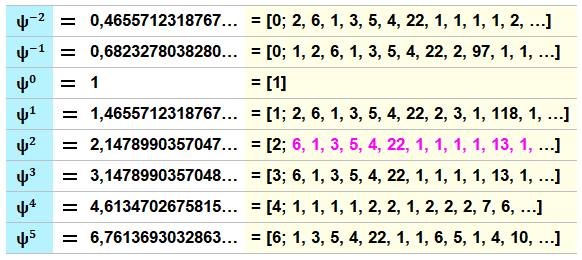
Valeurs des puissances, y compris
fractions continues
|
|
|
|
|
|
|
|
|
|
|
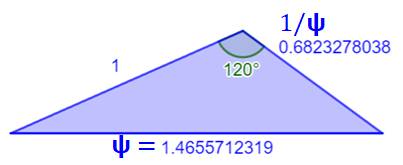
Triangle super doré L'angle est alors de 120° exactement. Les deux autres valent: |
|
|
|
Super rectangle doré Dans le rectangle 𝞇:1 la diagonale
vaut: Découper un carré 1:1. La largueur du nouveau
rectangle vaut: |
|
|
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |