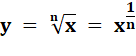|
||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
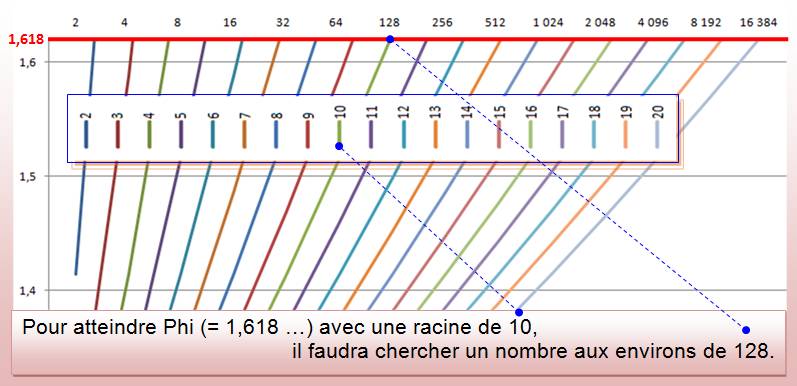
RACINES Approximations d'une constante Valeurs d'une racine énième
s'approchant de la valeur d'une constante donnée. Bonne idée d'exercice pour
apprivoiser les calculs avec logarithmes. Exemple: |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Calcul du logarithme de x et retour à x par exponentiation. |
ln(x) = 10 x ln(1,618 033 …)
= 10 x 0,481211…
= 4,81211 … x = exp(4,81211…) =
122,990… |
|
|
|
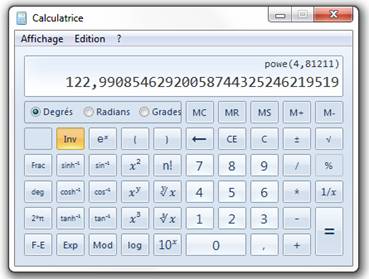
Exp(4,8211) s'obtient en tapant d'abord le nombre puis en cliquant
simplement sur "Inv" puis sur " ex ". |
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
Pour aller plus loin
Note:
|
||
|
|
|
|
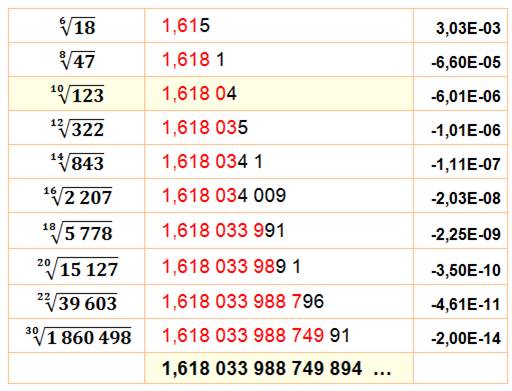
En gros, pour un écart
de 0,…e-n, il faut effectuer la racine 2n d'un nombre de n
chiffres. |
|
![]()
|
Suite |
|
|
C |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()