|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Méthode ou crible de René Nève Méthode
très originale qui se rapproche de celle de Sundaram.
Exploration des nombres pairs et des nombres impairs. En fait, ici, il s'agit
de leurs sommes. La méthode détecte les nombres premiers et factorise les
autres. Elle porte le nom du père de la
personne qui me la communiquée, à défaut de lui trouver une antériorité que
je n'ai pas trouvée ni dans la littérature ni sur Internet. |
|
|
||
|
La
méthode s'applique aux nombres impairs que l'on écrit sous
la forme. On va poursuivre avec la cas 4A + 1. |
N = 4A – 1 N = 4A + 1 |
|
|
L'astuce consiste
à exprimer le quotient(A) sous la forme de la différence entre un nombre
impair au carré et d'un nombre pair multiplié par son successeur. Si cette
expression de A existe, alors N est le produit de deux facteurs. |
A = p(p+1) – i² N = 4( p(p+1) – i² ) + 1 = 4p² + 4p – 4i² + 1 = f1 . f2 Avec f1 = 2(p – i) + 1 f2 = 2(p + i) + 1 |
|
|
Comment
trouver cette expression, En balayant les nombres pairs et les nombres
impairs en remarquant les identités
indiquées => |
i² = 1 + 3 + 5 + … somme des
impairs p(p+1) = 2 + 4 + 6 + … somme des pairs |
|
|
Exemple
Le nombre A = 14 est atteint avec 5x6 – 4² p = 5 et i = 4 => f1
= 2(1) + 1 = 3 et f2 = 2(9) + 1 = 19 n = f1 .f2 = 3 x 19 = 57 = 4 x 14
+ 1 |
||
|
|
||
|
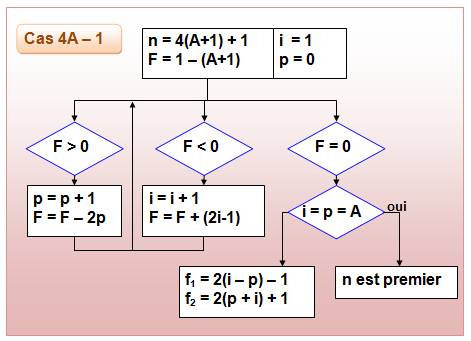
L'algorithme
va implémenter et balayer la table
indiquée ci-dessus en progressant sur les nombres pairs (p) et les nombres
impairs (i). F est une
variable de calcul que l'on cherche rendre nulle. Quatre
types d'actions selon la valeur de F (cas 4A + 1):
Les
valeurs sont adaptées selon que n = 4A + 1 ou 4A – 1. |
|
|
|
|
||
|
|
Le programme complet comprend deux
procédures et un programme d'utilisation. Procédure Aplus pour le cas n = 4A + 1. On retrouve les paramètres initialisés comme vu lors de la description
de l'algorithme. Le fait de renouveler les tests sur la valeur de F est implémenté sous
forme d'une boucle de paramètre k. On laisse faire au plus jusqu'à k = n,
mais cette progression est stoppée s'il y a conclusion (F= 0) . Alors k = n +
1, valeur dépassant celle autorisée pour la boucle. L'analyse F = 0 est opérée en premier avec ses deux conclusions
possibles. Si n est premier, pour uniformiser la sortie, on donne les deux
facteurs, 1 et n. Si F n'est pas nul, on fait progresser i ou p
selon le signe de F. Et F est mis à jour. Notez que la progression fait intervenir les pairs successifs et les
impairs successifs; basculant de l'un à l'autre selon le signe de F mis à
jour. Dans tous les cas, la procédure retourne trois nombres; n et les deux facteurs. La procédure Amoins est du même
type avec adaptation des paramètres. |
|
|
|
Le programme principal fait appel à ces
deux procédures selon la valeur de n. On prend la précaution d'éliminer le cas des nombres pairs. On calcule le quotient et le reste de la division de n par 4. Selon le reste on oriente vers l'une ou l'autre des procédures. Impression des résultats Nous avons demandé de tester les nombres impairs de 1005 à 1021. Le
programme principal nous indique que 1009, 1013, 1019 et 1021 sont premiers. Il donne deux facteurs pour les autres nombres. Vérification Ce court programme utilise les facilités du logiciel Maple qui teste
directement la primalité des nombres et en donne les facteurs. Confirmation de l'algorithme et du logiciel selon la méthode de René
Nève. |
|
Voir Programmation – Index
|
La
méthode est très rapide sans cependant égaler les méthodes modernes
implémentées dans les logiciels de calculs tels que Maple. Par
contre, elle est prodigieusement astucieuse. Bravo à la personne qui l'a
inventée qui que ce soit. "La
méthode ne nécessite pas la connaissance des nombres premiers. Elle est
facile à programmer: une division par 4, puis une série d'additions et, ou de
soustractions. Si le nombre à factoriser est premier le résultat est 1 et le
nombre lui même. Si le nombre à factoriser est le produit de 2 nombres
premiers, le calcul sera d'autant plus rapide qu'ils sont grands et proches
l'un de l'autre. Quasi instantané s’il s’agit de 2 nombres premiers
successifs. Michel Nève – Fils de René Nève |
|
|
|
|
Aplus := proc (A) local i, p,
f1, f2, F, k, n; i := 1; p := 1; F := 1-A; n := 4*A+1; for k while k < n
do if F = 0 then if p = i and i = A then f1 := 1; f2 := n else f1 :=
2*p-2*i+1; f2 := 2*p+2*i+1 end if; k := n+1 else if F < 0 then p := p+1; F
:= F+2*p else i := i+1; F := F-2*i+1 end if end if end do; return n, f1, f2
end proc; Amoins := proc (A) local i, p,
f1, f2, F, k, n; i := 1; p := 0; F := -A; n := 4*A+3; for k while k < n do
if F = 0 then if p = i and i = A+1 then f1 := 1; f2 := n else f1 :=
2*i-2*p-1; f2 := 2*p+2*i+1 end if; k := n+1 else if 0 < F then p := p+1; F
:= F-2*p else i := i+1; F := F+2*i-1 end if end if end do; return n, f1, f2
end proc; for n from 1005 by
2 to 1021 do if `mod`(n, 2) = 0 then lprint(n, pair) else Q := iquo(n, 4); R
:= irem(n, 4); if R = 1 then lprint(Aplus(Q)) else lprint(Amoins(Q)) end if
end if end do; Copier ce texte dans Maple (Crtl C puis
Ctrl V). Faire "entrée" successivement sur
le texte de chacun de ces trois programmes. |
|
![]()
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Cette page |
![]()