|
Édition du: 27/10/2021 |
|
INDEX Nombres
(Classification) |
CRIBLES (Sieves) |
|||
![]()
|
CRIBLE de MOESSNER Théorème de Moessner, construction
de Moessner Méthode
de construction des puissances
des nombres à partir de la suite des entiers et
en procédant à des additions
sélectives. Elle fut découverte
en 1951 par Alfred Moessner et prouvée la même année par Oskar Perron. La
démonstration du désormais théorème fait appel à la combinatoire
des coefficients
binomiaux. Il existe
deux extensions de ce théorème:
Récemment
Dexter Kozen et Alexandra Silva ont prouvé un théorème général qui englobe
celui de Moessner et toutes les autres généralisations. |
||
|
|
Sommaire de cette page >>> Construction du triangle de Pascal >>> Construction des triangles des puissances >>> Construction du triangle des carrés >>> Interprétation géométrique >>> Interprétation arithmétique >>> Théorème de Moessner >>> Construction des factorielles |
Débutants Glossaire |
Titre de la publication
|
Eine Bemerkung über die Potenzen der natürlichen Zahlen Une remarque sur les puissances des nombres naturels. Von Alfred Moessner in Gunzenhausen
am 2. März 1951 Gunzenhauzen est une ville de Bavière (Allemagne) |
|
Construction La construction classique du triangle
de Pascal se présente avec le sommet du triangle en haut au milieu. Ici, le sommet est en haut à gauche et chaque
nombre est égal à la somme de celui-du haut avec celui de gauche. On commence la construction en alignant des
"1". |
Le triangle de Pascal
|
||
|
Construction répétée Une extension consiste utiliser le même procédé
en ignorant un "1" de temps en temps. Sur cet exemple, on saute un "1" sur
cinq. La somme est toujours réalisée avec
le nombre du dessus et celui présent à gauche (ex: 5 = 1 + 4 ou 81 = 65 +
16). |
Multi-triangle de Pascal
|
||
|
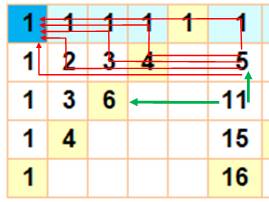
Interprétation Les nombres qui figurent dans ce tableau indiquent
la quantité de chemins possibles pour aller de cette cellule à la cellule
d'origine (bleu foncé). Depuis le "11", on peut rejoindre
l'origine selon le chemin horizontal (6 possibilités) et le chemin vertical
(5 possibilités, développées en rouge)).
En fait, la quantité de chemin est égale à la
somme des chemins hérités par le haut et par la gauche. |
|
||
|
Construction des cubes Le même procédé est appliqué, à la différence
près que l'on ignore un nombre sur trois, mais sur la deuxième ligne. La ligne 1 produit la suite des nombres entiers. Sur la deuxième ligne, on continue à additionner
"haut" et "gauche", mais en sautant un nombre sur trois.
Dit autrement: on ignore les multiples de 3. |
Le triangle des cubes
Ligne 0: suite de
"1". Ligne 1: somme des nombres
"haut" et "bas". Ligne 2: même type de sommes
en ignorant un nombre sur trois. Ligne 3: sommes poursuivant la
construction des triangles, donc en ignorant un nombre supplémentaire. Arrêt lorsque les triangles
sont complets. En l'occurrence, les nombres du bas sont les cubes
des nombres entiers successifs. |
||
|
Et les puissances 4 ? Le procédé fonctionne. Il suffit d'ignorer un
nombre sur quatre. La ligne 4 produit les puissances quatrièmes des
nombres successifs |
Le triangle des bicarrés
|
||
Voir Brève
771
|
Construction des carrés Oui ! Le même procédé fonctionne pour les carrés
en ignorant un nombre sur deux. C'est le cas le plus simple et qui est très
connu: Un carré
est la somme cumulée des nombres impairs. |
Le triangle des carrés
|
|
|
Somme des impairs = carré Il existe une image bien connue pour la somme des
impairs qui produit les nombres au carré. La forme en L ajoutée représente un nombre
impair. (Un gnomon) Somme des cubes On peut représenter la somme des cubes. Après le
cube unité vient le cube du nombre 2 = 8. Sa représentation est composée de trois éléments:
Le cube suivant est 27 = 8 + 19 qui s'explique
moins bien. En revanche, la formule de calcul – Somme des entiers sauf les multiples de 3
– s'explique simplement avec les identités remarquables: (Voir le tableau
ci-contre et les explications sur la page des cubes). En général Il est bien difficile d'imaginer une
représentation géométrique avec des dimensions plus grandes. |
Construction des carrés
Construction des cubes
|
|||||||||||||||||||
|
Prenons le cas des bicarrés et intéressons-nous
aux diagonales finales dans chaque triangle.
On y reconnait la trace de la rangée 4 du
triangle de Pascal, autrement-dit les coefficients binomiaux d'ordre 4.
Nous sommes sur la piste de la démonstration,
laquelle implique la manipulation des coefficients binomiaux. Un calcul
opératoire que vous trouverez sur la page d'Olivier
Rousselot. |
|
|
Pour chaque entier positif k (k >
1), si tous les kièmes nombres sont ignorés dans la ligne 1, chaque (k – 1)ièmes nombre dans la ligne 2, et,
d'une manière générale, chaque (k + 1 – i)ème nombre dans la ligne i, alors
la ligne k de ces sommes partielles seront la puissance k des nombres entiers
successifs. Anglais
|
|
Construction des factorielles Oui ! Le même procédé est utilisé. Cependant, l'espace entre les nombres ignorés
n'est pas régulier; il est incrémenté. On conserve donc un nombre, puis deux, puis
trois, etc. Autres Libre
imagination pour trouver bien d'autres propriétés. L'une d'entre-elle
consiste engendrer des progressions
arithmétiques. |
Le triangle des factorielles
|
|
Merci
à Daniel Silvia Fuks pour l'idée de cette page
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Vidéo |
|
|
Cette page |